
【题目】已知抛物线![]() :
:![]() 和直线
和直线![]() :
:![]() ,
,![]() 是直线上
是直线上![]() 一点,过点
一点,过点![]() 做抛物线的两条切线,切点分别为
做抛物线的两条切线,切点分别为![]() ,
,![]() ,
,![]() 是抛物线上异于
是抛物线上异于![]() ,
,![]() 的任一点,抛物线在
的任一点,抛物线在![]() 处的切线与
处的切线与![]() ,
,![]() 分别交于
分别交于![]() ,
,![]() ,则
,则![]() 外接圆面积的最小值为______.
外接圆面积的最小值为______.
科目:高中数学 来源: 题型:
【题目】2018年1月31日晚上月全食的过程分为初亏、食既、食甚、生光、复圆五个阶段,月食的初亏发生在19时48分,20时51分食既,21时29分食甚,22时07分生光,23时11分复圆.月全食伴随有蓝月亮和红月亮,全食阶段的“红月亮”在食既时刻开始,生光时刻结束.小明准备在19:55至21:56之间的某个时刻欣赏月全食,则他等待“红月亮”的时间不超过30分钟的概率是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一家公司生产某种品牌服装的年固定成本为![]() 万元,每生产
万元,每生产![]() 千件需另投入
千件需另投入![]() 万元.设该公司一年内共生产该品牌服装
万元.设该公司一年内共生产该品牌服装![]() 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为![]() 万元,且
万元,且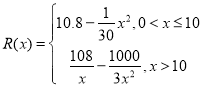 .
.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获得利润最大?(注:年利润=年销售收入-年总成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=3sin(﹣3x![]() )﹣2的图象向右平移
)﹣2的图象向右平移![]() 个单位长度得到函数g(x)的图象,若g(x)在区间[
个单位长度得到函数g(x)的图象,若g(x)在区间[![]() ,θ]上的最大值为1,则θ的最小值为( )
,θ]上的最大值为1,则θ的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
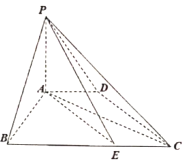
【题目】已知四棱锥![]() 中,底面
中,底面![]() 为等腰梯形,
为等腰梯形,![]() ,
,![]() ,
,![]() ,
,![]() 丄底面
丄底面![]() .
.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)过![]() 的平面交
的平面交![]() 于点
于点![]() ,若平面
,若平面![]() 把四棱锥
把四棱锥![]() 分成体积相等的两部分,求二面角
分成体积相等的两部分,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com