
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 是矩形,
是矩形,![]() ,
,![]() 是
是![]() 的中点.
的中点.
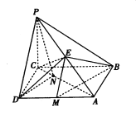
(1)求证:![]() 平面
平面![]() ;
;
(2)已知点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 上一点,且平面
上一点,且平面![]() 平面
平面![]() .若
.若![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,
(1)试证明函数![]() 是偶函数;
是偶函数;
(2)画出![]() 的图象;(要求先用铅笔画出草图,再用黑色签字笔描摹,否则不给分)
的图象;(要求先用铅笔画出草图,再用黑色签字笔描摹,否则不给分)
(3)请根据图象指出函数![]() 的单调递增区间与单调递减区间;(不必证明)
的单调递增区间与单调递减区间;(不必证明)
(4)当实数![]() 取不同的值时,讨论关于
取不同的值时,讨论关于![]() 的方程
的方程![]() 的实根的个数;(不必求出方程的解)
的实根的个数;(不必求出方程的解)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C所对应的边分别为a,b,c.
(Ⅰ)若a,b,c成等差数列,证明:sinA+sinC=2sin(A+C);
(Ⅱ)若a,b,c成等比数列,求cosB的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(π﹣ωx)cosωx+cos2ωx(ω>0)的最小正周期为π.
(Ⅰ)求ω的值;
(Ⅱ)将函数y=f(x)的图象上各点的横坐标缩短到原来的![]() ,纵坐标不变,得到函数y=g(x)的图象,求函数y=g(x)在区间
,纵坐标不变,得到函数y=g(x)的图象,求函数y=g(x)在区间![]() 上的最小值.
上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了参加市高中篮球比赛,某中学决定从四个篮球较强的班级的篮球队员中选出![]() 人组成男子篮球队,代表该地区参赛,四个篮球较强的班级篮球队员人数如下表:
人组成男子篮球队,代表该地区参赛,四个篮球较强的班级篮球队员人数如下表:
班级 | 高三(7)班 | 高三(17)班 | 高二(31)班 | 高二(32)班 |
人数 | 12 | 6 | 9 | 9 |
(1)现采取分层抽样的方法从这四个班中抽取运动员,求应分别从这四个班抽出的队员人数;
(2)该中学篮球队奋力拼搏,获得冠军.若要从高三年级抽出的队员中选出两位队员作为冠军的代表发言,求选出的两名队员来自同一班的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校某研究性学习小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数![]() 与听课时间
与听课时间![]() (单位:分钟)之间的关系满足如图所示的图象,当
(单位:分钟)之间的关系满足如图所示的图象,当![]() 时,图象是二次函数图象的一部分,其中顶点
时,图象是二次函数图象的一部分,其中顶点![]() ,过点
,过点![]() ;当
;当![]() 时,图象是线段
时,图象是线段![]() ,其中
,其中![]() .根据专家研究,当注意力指数大于62时,学习效果最佳.
.根据专家研究,当注意力指数大于62时,学习效果最佳.

(1)试求![]() 的函数关系式;
的函数关系式;
(2)教师在什么时段内安排内核心内容,能使得学生学习效果最佳?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是 .(填序号)
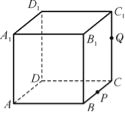
①当0<CQ<![]() 时,S为四边形;
时,S为四边形;
②当CQ=![]() 时,S为等腰梯形;
时,S为等腰梯形;
③当CQ=![]() 时,S与C1D1的交点R满足C1R=
时,S与C1D1的交点R满足C1R=![]() ;
;
④当![]() <CQ<1时,S为六边形;
<CQ<1时,S为六边形;
⑤当CQ=1时,S的面积为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 和圆
和圆![]() .
.

(1)若直线![]() 过点
过点![]() ,且被圆
,且被圆![]() 截得的弦长为
截得的弦长为![]() 是,求直线
是,求直线![]() 的方程;
的方程;
(2)设![]() 为平面上的点,满足:存在过点
为平面上的点,满足:存在过点![]() 的无穷多对互相垂直的直线
的无穷多对互相垂直的直线![]() 和
和![]() ,它们分别与圆
,它们分别与圆![]() 和圆
和圆![]() 相交,且直线
相交,且直线![]() 与被圆
与被圆![]() 截得的弦长与直线
截得的弦长与直线![]() 被圆
被圆![]() 截得的弦长相等,试求所有满足条件的点
截得的弦长相等,试求所有满足条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com