练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】将圆每一点的横坐标保持不变，纵坐标变为原来的倍，得到曲线.

    （1）写出的参数方程；

    （2）设直线与的交点为，以坐标原点为极点， 轴的正半轴为极轴建立极坐标系，求：过线段的中点且与垂直的直线的极坐标方程.

    【答案】（1）（t为参数）．（2）

    【解析】试题分析：（1）根据变换得，再利用三角换元得（2）先求出直角坐标方程：由直线方程与椭圆方程解得交点坐标P1（2，0），P2（0，1），得中点坐标，利用点斜式得直线方程，最后根据得极坐标方程

    试题解析：（I）设（x1，y1）为圆上的点，在已知变换下变为C上点（x，y），

    依题意得：圆的参数方程为（t为参数）

    所以C的参数方程为（t为参数）．

    （II）由解得或

    所以P1（2，0），P2（0，1），则线段P1P2的中点坐标为，所求直线的斜率k＝，于是所求直线方程为，并整理得

    化为极坐标方程， ，即.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数，

    （1）若，求函数的零点；

    （2）若函数在区间上恰有一个零点，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

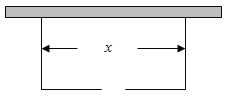
    【题目】围建一个面积为360的矩形场地，要求矩形场地的一面利用旧墙（利用旧墙需维修），其它三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2m的进出口，如图所示，已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为（单位：），修建此矩形场地围墙的总费用为（单位：元）

    （1）将表示为的函数；

    （2）试确定,使修建此矩形场地围墙的总费用最小，并求出最小总费用。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

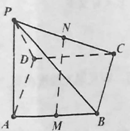
    【题目】如图所示, 平面，四边形是矩形，，分别是的中点．

    （1）求平面和平面所成二面角的大小；

    （2）求证: 平面；

    （3）当的长度变化时, 求异面直线与所成角的可能范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下面说法:

    ①如果一组数据的众数是，那么这组数据中出现次数最多的数是；

    ②如果一组数据的平均数是, 那么这组数据的中位数为；

    ③如果一组数据的的中位数 , 那么；

    ④如果一组数据的平均数是正数, 那么这组数据都是正数．

    其中错误的个数是（ ）

    A． B． C． D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆：（）的两个焦点与短轴的一个端点是直角三角形的三个顶点，直线：与椭圆有且只有一个公共点.

    （1）求椭圆的方程及点的坐标；

    （2）设为坐标原点，直线平行于，与椭圆交于不同的两点，且与直线交于点.证明：存在实数，使得，并求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数的函数图象在点处的切线平行于轴.

    （1）求函数的极值；

    （2）若直线与函数的图象交于两点，求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】5名乒乓球队员中，有2名老队员和3名新队员，现从中选出3名队员排成1、2、3号参加团体比赛，则入选的3名队员中至少有一名老队员,且1、2号中至少有1名新队员的排法有（ ）种

    A. 72 B. 63 C. 54 D. 48

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数为奇函数，且相邻两对称轴间的距离为.

    （1）当时，求的单调递减区间；

    （2）将函数的图象沿轴方向向右平移个单位长度，再把横坐标缩短到原来的（纵坐标不变），得到函数的图象.当时，求函数的值域.

    查看答案和解析>>

    同步练习册答案