
已知直线l:y=x+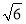 ,圆O:x2+y2=5,椭圆E:
,圆O:x2+y2=5,椭圆E: =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,直线l被圆O截得的弦长与椭圆的短轴长相等.
,直线l被圆O截得的弦长与椭圆的短轴长相等.
(1)求椭圆E的方程;
(2)过圆O上任意一点P作椭圆E的两条切线,若切线都存在斜率,求证:两条切线的斜率之积为定值.
(1)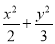 =1(2)-1.
=1(2)-1.
【解析】(1)设椭圆的半焦距为c,圆心O到直线l的距离d=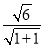 =
= ,∴b=
,∴b= =
=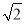 ,由题意,得
,由题意,得 ∴a2=3,b2=2.∴椭圆E的方程为
∴a2=3,b2=2.∴椭圆E的方程为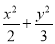 =1.
=1.
(2)设点P(x0,y0),过点P的椭圆E的切线l0的方程为y-y0=k(x-x0),
联立直线l0与椭圆E的方程,得
消去y,得(3+2k2)x2+4k(y0-kx0)x+2(kx0-y0)2-6=0,
∴Δ=[4k(y0-kx0)]2-4(3+2k2)[2(kx0-y0)2-6]=0,整理,得(2-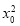 )k2+2kx0y0-(
)k2+2kx0y0-(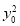 -3)=0,设满足题意的椭圆E的两条切线的斜率分别为k1,k2,
-3)=0,设满足题意的椭圆E的两条切线的斜率分别为k1,k2,
则k1·k2=-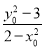 .∵点P在圆O上,∴
.∵点P在圆O上,∴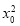 +
+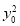 =5.
=5.
∴k1·k2=- =-1.∴两条切线的斜率之积为常数-1.
=-1.∴两条切线的斜率之积为常数-1.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练16练习卷(解析版) 题型:选择题
已知抛物线y2=4x,圆F:(x-1)2+y2=1,过点F作直线l,自上而下顺次与上述两曲线交于点A,B,C,D(如图所示),则|AB|·|CD|的值正确的是( ).

A.等于1 B.最小值是1 C.等于4 D.最大值是4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练12练习卷(解析版) 题型:填空题
设α和β为两个不重合的平面,给出下列四个命题:
①若α内的两条相交直线分别平行于β内的两条直线,则α平行于β;②若α外一条直线l与α内的一条直线平行,则l和α平行;③设α和β相交于直线l,若α内有一条直线垂直于l,则α和β垂直;④直线l与α垂直的充分必要条件是l与α内的两条直线垂直.其中为真命题的是________(写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练10练习卷(解析版) 题型:解答题
已知首项为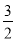 的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
(1)求数列{an}的通项公式;
(2)设Tn=Sn- (n∈N*),求数列{Tn}的最大项的值与最小项的值.
(n∈N*),求数列{Tn}的最大项的值与最小项的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练10练习卷(解析版) 题型:选择题
已知首项为正数的等差数列{an}的前n项和为Sn,若a1 006和a1 007是方程x2-2 012x-2 011=0的两根,则使Sn>0成立的正整数n的最大值是( ).
A.1006 B.1007 C.2011 D.2012
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷5练习卷(解析版) 题型:填空题
设圆x2+y2=2的切线l与x轴正半轴、y轴正半轴分别交于点A,B,当|AB|取最小值时,切线l的方程为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷5练习卷(解析版) 题型:选择题
已知圆x2+y2-4x-9=0与y轴的两个交点A,B都在某双曲线上,且A,B两点恰好将此双曲线的焦距三等分,则此双曲线的标准方程为( ).
A. 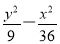 =1 B.
=1 B. =1 C.
=1 C. =1 D.
=1 D. 
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷4练习卷(解析版) 题型:选择题
已知正方体ABCD-A1B1C1D1,M为棱A1B1的中点,N为棱A1D1的中点.如图是该正方体被M,N,A所确定的平面和N,D,C1所确定的平面截去两个角后所得的几何体,则这个几何体的正视图为( ).

查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷1练习卷(解析版) 题型:选择题
记△ABC各边的中点分别为D,E,F,在A,B,C,D,E,F中任取4点,若这4点为平行四边形顶点,则称为选取成功.某人连续进行3次这种选取,则至少成功1次的概率是( ).
A.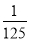 B.
B.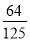 C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com