
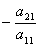
思路解析:本例是把实际问题解决抽象成二元一次方程组的求解问题,求解二元一次方程组有两种算法:(1)首先讲清高斯消去法的思路.(2)把高斯消去法用算法表述出来.(3)提示学生分析解题的关键所在,再用公式法表示出来.从二元一次方程组的算法知:求解某个问题的算法不是唯一的.
解:方法一:
第一步:假定a11≠0,⑴×(![]() )+⑵,得(a22-
)+⑵,得(a22-![]() )x2=b2-
)x2=b2-![]() .
.
原方程组化为
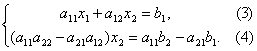
第二步:如果a11a22-a21a12=0,输出方程组无解或有无数组解.
如果a11a22-a21a12≠0,解⑷得x2=![]() . ⑸
. ⑸
第三步:将⑸代入⑶,整理得x1=![]() . ⑹
. ⑹
第四步:输出结果x1、x2,方程组无解或有无数组解.
方法二:第一步:计算D=a11a22-a21a12.
第二步:若D=0,输出方程组无解或有无数组解,否则(D≠0)时,
x1=![]() ,
,
x2=![]() .
.
第三步:输出结果x1,x2、方程组无解或有无数组解.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源:2009年高考数学第二轮复习热点专题测试卷:算法初步(含详解) 题型:022
写出解二元一次方程组![]() 的一个算法:第一步:(2)×2+(1)得:x=2;第二步:________;第三步:输出x,y的值.
的一个算法:第一步:(2)×2+(1)得:x=2;第二步:________;第三步:输出x,y的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com