
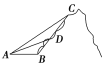
【题目】如图,嵩山上原有一条笔直的山路BC,现在又新架设了一条索道AC,小李在山脚B处看索道AC,发现张角∠ABC=120°;从B处攀登400米到达D处,回头看索道AC,发现张角∠ADC=150°;从D处再攀登800米方到达C处,则索道AC的长为________米.
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() 为常数,
为常数,![]() ).(Ⅰ)求函数
).(Ⅰ)求函数![]() 的单调区间;(Ⅱ)当
的单调区间;(Ⅱ)当![]() 时,是否存在实数
时,是否存在实数![]() ,使得当
,使得当![]() 时,不等式
时,不等式![]() 恒成立?如果存在,求
恒成立?如果存在,求![]() 的取值范围;如果不存在,请说明理由(其中
的取值范围;如果不存在,请说明理由(其中![]() 是自然对数的底数,
是自然对数的底数,![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】做投掷2个骰子试验,用(x,y)表示点P的坐标,其中x表示第1个骰子出现的点数,y表示第2个骰子出现的点数.
(1)求点P在直线y=x上的概率.
(2)求点P不在直线y=x+1上的概率.
(3)求点P的坐标(x,y)满足16<x2+y2≤25的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知三棱锥P-ABC,∠ACB=90°,CB=4,AB=20,D为AB的中点,且△PDB是正三角形,PA⊥PC.
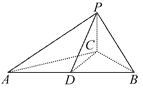
(1)求证:平面PAC⊥平面ABC.
(2)求二面角D-AP-C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O![]() 的直径,FB是圆台的一条母线.
的直径,FB是圆台的一条母线.
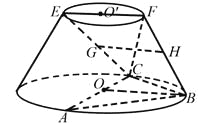
(Ⅰ)已知G,H分别为EC,FB的中点,求证:GH∥平面ABC;
(Ⅱ)已知EF=FB=![]() AC=
AC=![]() ,AB=BC.求二面角
,AB=BC.求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台在一次对收看文艺节目和新闻节目的抽样调查中,随机抽取了100名电视观众,相关的数据如表所示:
类别 | 文艺节目 | 新闻节目 | 总计 |
20至40岁 | 40 | 18 | 58 |
大于40岁 | 15 | 27 | 42 |
总计 | 55 | 45 | 100 |
(1)由表中数据直观分析,收看新闻节目的观众是否与年龄有关?
(2)用分层抽样方法在收看新闻节目的观众中随机抽取5名,则大于40岁的观众应该抽取几名?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某班一次数学测试成绩的茎叶图(如图甲)和频率分布直方图(如图乙)都受到不同程度的污损,其中,频率分布直方图的分组区间分别为![]() ,据此解答如下问题.(注:直方图中
,据此解答如下问题.(注:直方图中![]() 与
与![]() 对应的长方形的高度一样)
对应的长方形的高度一样)
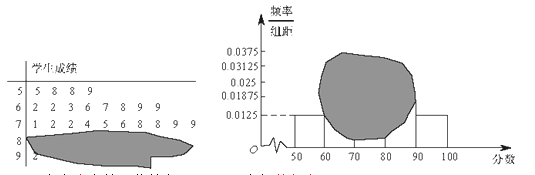
(1)若按题中的分组情况进行分层抽样,共抽取![]() 人,那么成绩在
人,那么成绩在![]() 之间应抽取多少人?
之间应抽取多少人?
(2)现从分数在![]() 之间的试卷中任取
之间的试卷中任取![]() 份分析学生失分情况,设抽取的试卷分数在
份分析学生失分情况,设抽取的试卷分数在![]() 之间 份数为
之间 份数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com