
 在(1+x+x2)n=D${\;}_{n}^{0}$+D${\;}_{n}^{1}$x+D${\;}_{n}^{2}$x2+…+D${\;}_{n}^{r}$xr+…D${\;}_{n}^{2n-1}$x2n-1+D${\;}_{n}^{2n}$x2n的展开式中,把D${\;}_{n}^{0}$,D${\;}_{n}^{1}$,D${\;}_{n}^{2}$,…,D${\;}_{n}^{2n}$叫做三项式系数.
在(1+x+x2)n=D${\;}_{n}^{0}$+D${\;}_{n}^{1}$x+D${\;}_{n}^{2}$x2+…+D${\;}_{n}^{r}$xr+…D${\;}_{n}^{2n-1}$x2n-1+D${\;}_{n}^{2n}$x2n的展开式中,把D${\;}_{n}^{0}$,D${\;}_{n}^{1}$,D${\;}_{n}^{2}$,…,D${\;}_{n}^{2n}$叫做三项式系数.分析 (Ⅰ)根据三项式(x2+x+1)2的展开式,写出对应三项式的系数即可;
(Ⅱ)类比杨辉三角,画出三项式的n(0≤n≤4)次系数的数阵表:
(Ⅲ)根据(1+x+x2)2016•(x-1)2016的展开式中x2016的系数,与二项式(x3-1)2016展开式中x2016的系数相等,求出对应代数式的值.
解答 解:(Ⅰ)因为(x2+x+1)2=x4+2x3+3x2+2x+1,
所以${D}_{2}^{0}$=1,${D}_{2}^{1}$=2,${D}_{2}^{2}$=3,${D}_{2}^{3}$=2,${D}_{2}^{4}$=1;…(3分)
(Ⅱ)类比杨辉三角,画出三项式的n(0≤n≤4)次系数的数阵表如下: …(6分)
…(6分)
(Ⅲ)(1+x+x2)2016•(x-1)2016
=(${D}_{2016}^{0}$+${D}_{2016}^{1}$x+${D}_{2016}^{2}$x2+…+${D}_{2016}^{r}$xr+…+${D}_{2016}^{4029}$x4029+${D}_{2016}^{4030}$x4030)
•(${C}_{2016}^{0}$x2016-${C}_{2016}^{1}$x2015+${C}_{2016}^{2}$x2014-${C}_{2016}^{3}$x3+…+(-1)r${C}_{2016}^{r}$x2016-r+…-${C}_{2016}^{2015}$x+${C}_{2016}^{2016}$),
其中x2016的系数为
${D}_{2016}^{0}$${C}_{2016}^{0}$-${D}_{2016}^{1}$${C}_{2016}^{1}$+${D}_{2016}^{2}$${C}_{2016}^{2}$-${D}_{2016}^{3}$${C}_{2016}^{3}$+…+${D}_{2016}^{2016}$${C}_{2016}^{2016}$,
又(1+x+x2)2016•(x-1)2016=(x3-1)2016,
而二项式(x3-1)2016的通项公式为
Tr+1=(-1)r${C}_{2016}^{r}$(x3)2016-r,
由3×(2016-r)=2016解得r=1344,
所以x2016系数为${C}_{2016}^{1344}$=${C}_{2016}^{672}$;
由代数式恒成立,得
${D}_{2016}^{0}$${C}_{2016}^{0}$-${D}_{2016}^{1}$${C}_{2016}^{1}$+${D}_{2016}^{2}$${C}_{2016}^{2}$-${D}_{2016}^{3}$${C}_{2016}^{3}$+…+${D}_{2016}^{2016}$${C}_{2016}^{2016}$=${C}_{2016}^{1344}$=${C}_{2016}^{672}$.…(14分)
点评 本题考查了推理与证明的应用问题,也考查了二项式定理的应用问题,考查了构造函数解答问题的能力,是综合性题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $({\frac{4}{9},+∞})$ | B. | $({\frac{4}{9},\frac{1}{2}})$ | C. | $({\frac{4}{9},\frac{1}{2}}]$ | D. | $({-∞,\frac{4}{9}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | α=kπ-$\frac{π}{3}$(k∈Z) | B. | α=kπ-$\frac{π}{6}$(k∈Z) | C. | α=kπ+$\frac{π}{3}$(k∈Z) | D. | α=kπ+$\frac{π}{6}$(k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
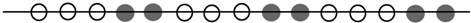
| A. | 白色 | B. | 黑色 | C. | 白色的可能性大 | D. | 黑色的可能性大 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
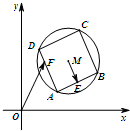 如图,已知圆M:(x-3)2+(y-3)2=4,四边形ABCD为圆M的内接正方形,E为边AB的中点,当正方形ABCD绕圆心M转动,同时点F在边AD上运动时,$\overrightarrow{ME}$$•\overrightarrow{OF}$的最大值是8.
如图,已知圆M:(x-3)2+(y-3)2=4,四边形ABCD为圆M的内接正方形,E为边AB的中点,当正方形ABCD绕圆心M转动,同时点F在边AD上运动时,$\overrightarrow{ME}$$•\overrightarrow{OF}$的最大值是8.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com