
分析 (1)利用三种方程的互化方法,求直线l的直角坐标方程和圆C的普通方程;
(2)若直线l与圆C有公共点,圆心到直线l的距离小于等于半径,即可求实数m的取值范围.
解答 解:(1)直线l的极坐标方程为$ρsin(θ+\frac{π}{3})=m$,直线l的直角坐标方程为$\sqrt{3}x+y-2m=0$,
圆C的参数方程为$\left\{\begin{array}{l}x=2+2cost\\ y=2sint\end{array}$(t为参数),圆C的普通方程为(x-2)2+y2=4;
(2)设圆心到直线l的距离为d,则d=$\frac{|2\sqrt{3}-2m|}{2}≤2$,
∴-2+$\sqrt{3}≤m≤2+\sqrt{3}$.
点评 本题考查三种方程的互化方法,考查直线与圆的位置关系,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,2] | B. | $[-\frac{5}{2},+∞)$ | C. | $(-∞,-\frac{5}{2})∪(2,+∞)$ | D. | $(-∞,-\frac{5}{2}]∪[2,+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
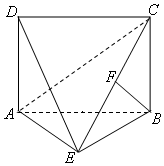 如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.
如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,1) | B. | (-1,3) | C. | (1,+∞) | D. | (-∞,-3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com