
【题目】【2017南通一模19】已知函数![]() 。
。
(1)当![]() 时,求函数
时,求函数![]() 的最小值;
的最小值;
(2)若![]() ,证明:函数
,证明:函数![]() 有且只有一个零点;
有且只有一个零点;
(3)若函数![]() 又两个零点,求实数
又两个零点,求实数![]() 的取值范围.
的取值范围.
【答案】见解析
【解析】解:(1)当![]() 时,
时,![]() ,
,
所以![]() ,
,
令![]() =0,得
=0,得![]() ,
,
当![]() 时,
时,![]() <0,当
<0,当![]() 时,
时,![]() >0,
>0,
所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以当![]() 时,
时,![]() 有最小值
有最小值![]() ;
;
(2)由![]() ,得:
,得:![]()
所以当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递减,
上单调递减,
所以当![]() 时,函数
时,函数![]() 在
在![]() 上最多有一个零点,
上最多有一个零点,
又当![]() 时,
时,![]() ,
,
所以当![]() 时,函数
时,函数![]() 在
在![]() 上有零点,
上有零点,
综上,当![]() 时,函数
时,函数![]() 有且只有一个零点;
有且只有一个零点;
(3)由(2)知:当![]() 时,函数
时,函数![]() 在
在![]() 上最多有一个零点,
上最多有一个零点,
因为函数![]() 有两个零点,所以
有两个零点,所以![]() ,9分
,9分
由![]() ,得:
,得:![]()
令![]() ,因为
,因为![]() ,
,
所以函数![]() 在
在![]() 上有且只有一个零点,设为
上有且只有一个零点,设为![]() ,
,
当![]() 时,
时,![]() <0,
<0,![]() <0,当时
<0,当时![]() ,
,![]() >0,
>0,![]() >0,
>0,
所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
要使得函数![]() 在
在![]() 上有两个零点,只需要函数
上有两个零点,只需要函数![]() 的最小值
的最小值![]() ,
,
即![]() ,又因为
,又因为![]() ,
,
消去![]() 得:
得:![]() ,
,
又因为![]() 在
在![]() 上单调递增,且
上单调递增,且![]() ,所以
,所以![]() >1,
>1,
则![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
所以2![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,13分
,13分
以下验证当![]() 时,函数
时,函数![]() 有两个零点。
有两个零点。
当![]() 时,
时,![]() ,所以
,所以![]() ,
,
因为![]() ,且
,且![]() ,
,
所以函数![]() 在
在![]() 上有一个零点,
上有一个零点,
又因为![]() (因为
(因为![]() ),且
),且![]() ,
,
所以函数![]() 在
在![]() 上有一个零点,
上有一个零点,
所以当![]() 时,函数
时,函数![]() 在
在![]() 上有两个零点。
上有两个零点。
综上,实数![]() 的取值范围是
的取值范围是![]() 。1
。1


科目:高中数学 来源: 题型:
【题目】【2017江西上饶联考】某种药种植基地有两处种植区的药材需在下周一、周二两天内采摘完毕,基地员工一天可以完成一处种植区的采摘,由于下雨会影响药材的收益,若基地收益如下表所示:已知下周一和下周二无雨的概率相同且为![]() ,两天是否下雨互不影响,若两天都下雨的概率为
,两天是否下雨互不影响,若两天都下雨的概率为![]()

(1)求![]() 及基地的预期收益;
及基地的预期收益;
(2)若该基地额外聘请工人,可在周一当天完成全部采摘任务,若周一无雨时收益为![]() 万元,有雨时收益为
万元,有雨时收益为![]() 万元,且额外聘请工人的成本为
万元,且额外聘请工人的成本为![]() 元,问该基地是否应该额外聘请工人,请说明理由.
元,问该基地是否应该额外聘请工人,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了增强环保意识,我校从男生中随机抽取了60人,从女生中随机抽取了50人参加环保知识测试,统计数据如下表所示:
优秀 | 非优秀 | 总计 | |
男生 | 40 | 20 | 60 |
女生 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
(1)试判断是否有99%的把握认为环保知识是否优秀与性别有关;
(2)为参加市里举办的环保知识竞赛,学校举办预选赛,已知在环保测试中优秀的同学通过预选赛的概率为 ![]() ,现在环保测试中优秀的同学中选3人参加预选赛,若随机变量X表示这3人中通过预选赛的人数,求X的分布列与数学期望.
,现在环保测试中优秀的同学中选3人参加预选赛,若随机变量X表示这3人中通过预选赛的人数,求X的分布列与数学期望.
附:K2= ![]()
P(K2≥k) | 0.500 | 0.400 | 0.100 | 0.010 | 0.001 |
k | 0.455 | 0.708 | 2.706 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn=n2 , {bn}为等比数列,且a1=b1 , b2(a2﹣a1)=b1 .
(1)求数列{an},{bn}的通项公式.
(2)设cn=anbn , 求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题p:直线y=kx+3与圆x2+y2=1相交于A,B两点;命题q:曲线![]() ﹣
﹣![]() =1表示焦点在y轴上的双曲线,若p∧q为真命题,求实数k的取值范围.
=1表示焦点在y轴上的双曲线,若p∧q为真命题,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【南京市、盐城市2017届高三年级第二次模拟】(本小题满分16分)
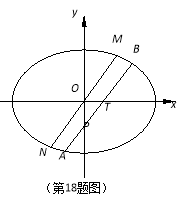
如图,在平面直角坐标系xOy中,焦点在x轴上的椭圆C:+=1经过点(b,2e),其中e为椭圆C的离心率.过点T(1,0)作斜率为k(k>0)的直线l交椭圆C于A,B两点(A在x轴下方).
(1)求椭圆C的标准方程;
(2)过点O且平行于l的直线交椭圆C于点M,N,求的值;
(3)记直线l与y轴的交点为P.若=,求直线l的斜率k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=x2+bx+c(其中b,c为实常数).
(1)若b>2,且y=f(sinx)(x∈R)的最大值为5,最小值为﹣1,求函数y=f(x)的解析式;
(2)是否存在这样的函数y=f(x),使得{y|y=x2+bx+c,﹣1≤x≤0}=[﹣1,0],若存在,求出函数y=f(x)的解析式;若不存在,请说明理由.
(3)记集合A={x|f(x)=x,x∈R},B={x|f(f(x))=x,x∈R}.
①若A≠,求证:B≠;
②若A=,判断B是否也为空集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【扬州市2016—2017学年度第一学期期末检测】(本小题满分14分)
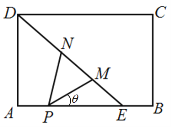
如图,矩形ABCD是一个历史文物展览厅的俯视图,点E在AB上,在梯形BCDE区域内部展示文物,DE是玻璃幕墙,游客只能在![]() ADE区域内参观.在AE上点P处安装一可旋转的监控摄像头,
ADE区域内参观.在AE上点P处安装一可旋转的监控摄像头,![]() 为监控角,其中M、N在线段DE(含端点)上,且点M在点N的右下方.经测量得知:AD=6米,AE=6米,AP=2米,
为监控角,其中M、N在线段DE(含端点)上,且点M在点N的右下方.经测量得知:AD=6米,AE=6米,AP=2米,![]() .记
.记![]() (弧度),监控摄像头的可视区域
(弧度),监控摄像头的可视区域![]() PMN的面积为S平方米.
PMN的面积为S平方米.
(1)求S关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;(参考数据:
的取值范围;(参考数据:![]() )
)
(2)求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国谜语大会》是中央电视台科教频道的一档集文化、益智、娱乐为一体的大型电视竞猜节目,目的是为弘扬中国传统文化、丰富群众文化生活.为选拔选手参加“中国谜语大会”,某地区举行了一次“谜语大赛”活动.为了了解本次竞赛选手的成绩情况,从中抽取了部分选手的分数(得分取正整数,满分为100分)作为样本进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100)的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出得分在[50,60),[90,100)的数据). 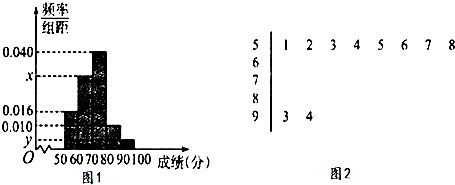
(1)求样本容量n和频率分布直方图中的x,y的值;
(2)分数在[80,90)的学生中,男生有2人,现从该组抽取三人“座谈”,求至少有两名女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com