
分析 (Ⅰ)设f(x)=ax2+bx+c,结合f(0)=1,f(x+1)-f(x)=2x,可得f(x)的解析式;
(Ⅱ)令2x=t,-1≤x≤1,结合二次函数的图象和性质,可得f(2x)在区间[-1,1]上的最大值与最小值.
解答 (本小题满分12分)
解:(Ⅰ)设f(x)=ax2+bx+c,-----------------------(1分)
由f(0)=1,得c=1,----------------------------------(2分)
由f(x+1)-f(x)=2x,得$\left\{\begin{array}{l}f(1)=f(0)=1\\ f(2)=f(1)+2=3\end{array}\right.$
解得a=1,b=-1--------------------------------------(5分)
所以,f(x)=x2-x+1--------------------------------(6分)
(Ⅱ)令2x=t,-1≤x≤1,
∴$\frac{1}{2}≤t≤2$------------------------------(8分)
$f(t)={t^2}-t+1={(t-\frac{1}{2})^2}+\frac{3}{4}(\frac{1}{2}≤t≤2)$---------------------------(10分)
所以${[f(t)]_{min}}=f(\frac{1}{2})=\frac{3}{4}$,此时x=-1;
[f(t)]max=f(2)=3,此时x=1------------------------------(12分)
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:选择题
| A. | 若l∥α,m∥α,则l∥m | B. | 若l⊥m,m?α,则l⊥α | C. | 若l∥α,m?α,则l∥m | D. | 若l⊥α,l∥m,则m⊥α |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
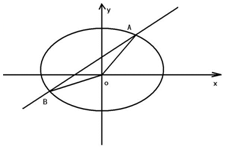 已知椭圆C的中心在坐标原点,一个焦点的坐标为$(\sqrt{3},0)$,椭圆C经过点P$(1,\frac{{\sqrt{3}}}{2})$.
已知椭圆C的中心在坐标原点,一个焦点的坐标为$(\sqrt{3},0)$,椭圆C经过点P$(1,\frac{{\sqrt{3}}}{2})$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(-n)<f(n-1)<f(n+1) | B. | f(n-1)<f(-n)<f(n+1) | C. | f(n+1)<f(-n)<f(n-1) | D. | f(n+1)<f(n-1)<f(-n) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com