
分析 命题P:关于x的不等式x2+ax+1>0对一切x∈R恒成立,可得△<0,解得a范围.命题q:方程$\frac{{x}^{2}}{a-4}$+$\frac{{y}^{2}}{a+2}$=1表示双曲线,可得(a-4)(a+2)<0,解得a范围.若p∨q为真命题,p∧q为假命题,可得p与q必然一真一假,即可得出.
解答 解:命题P:关于x的不等式x2+ax+1>0对一切x∈R恒成立,∴△=a2-4<0,解得-2<a<2.
命题q:方程$\frac{{x}^{2}}{a-4}$+$\frac{{y}^{2}}{a+2}$=1表示双曲线,∴(a-4)(a+2)<0,解得-2<a<4.
若p∨q为真命题,p∧q为假命题,
∴p与q必然一真一假,
∴$\left\{\begin{array}{l}{-2<a<2}\\{a≤-2或a≥4}\end{array}\right.$或$\left\{\begin{array}{l}{a≤-2或a≥2}\\{-2<a<4}\end{array}\right.$,
解得a∈∅或2≤a<4.
∴实数a的取值范围是[2,4).
点评 本题考查了一元二次不等式的解集与判别式的关系、双曲线的标准方程及其性质、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 仅一个零点且位于区间(c,+∞)内 | |
| B. | 仅一个零点且位于区间(-∞,a)内 | |
| C. | 有两个零点且分别位于区间(a,b)和(b,c)内 | |
| D. | 有两个零点且分别位于区间(-∞,a)和(c,+∞)内 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
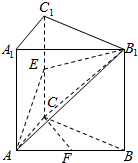 如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,AC=BC=1,AA1=2.
如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1的中点,AC=BC=1,AA1=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
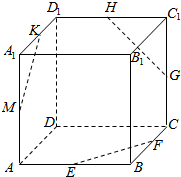 已知正方体ABCD-A1B1C1D1中,点E,F,G,H,K,M分别棱AB,BC,CC1,C1D1,A1D1,A1A的中点,如图,求证:EF,GH,KM共面.
已知正方体ABCD-A1B1C1D1中,点E,F,G,H,K,M分别棱AB,BC,CC1,C1D1,A1D1,A1A的中点,如图,求证:EF,GH,KM共面.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com