
【题目】已知数列{an}的前n项和为Sn,且Sn=n(n+2)(n∈N*).
(1)求数列{an}的通项公式;
(2)设bn![]() ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
【答案】(1)an=2n+1;(2)Tn![]() .
.
【解析】
(1)由n=1时求得a1,当n≥2时,由Sn=n(n+2)(n∈N*)① ,
可得Sn﹣1=(n﹣1)(n+1)② ,由①﹣②得an=2n+1,再检验当n=1时是否适合,求得an;
(2)由(1)求得bn![]() ,再利用错位相减法求其前n项和Tn即可.
,再利用错位相减法求其前n项和Tn即可.
解:(1)由题知:当n=1时,有S1=1×3=3=a1;
当n≥2时,由Sn=n(n+2)(n∈N*)① ,
可得Sn﹣1=![]() ② ,由①﹣② 得an=2n+1,
② ,由①﹣② 得an=2n+1,
又n=1时也适合,故an=2n+1;
(2)由(1)知bn![]() ,
,
∵Tn=3![]() 5
5![]() 7×(
7×(![]() )3+…+(2n+1)(
)3+…+(2n+1)(![]() )n③,
)n③,
∴![]() 3
3![]() 5×(
5×(![]() )3+…+(2n+1)
)3+…+(2n+1)![]() ④,
④,
由③﹣④可得:![]()

![]() ,
,
所以Tn![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】四位同学参加三项不同的竞赛.
(1)每位同学必须参加一项,有几种不同结果?
(2)每项竞赛只有且必须有一位同学参加,有几种不同结果?
(3)每位同学最多参加一项,且每项竞赛只许有一位同学参加,有几种不同结果?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且Sn=n﹣5an﹣85,n∈N*
(1)证明:{an﹣1}是等比数列;
(2)求数列{Sn}的通项公式.请指出n为何值时,Sn取得最小值,并说明理由?(参考数据![]() 15=﹣14.85)
15=﹣14.85)
查看答案和解析>>
科目:高中数学 来源: 题型:
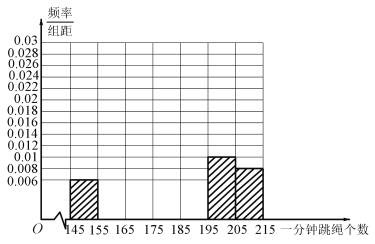
【题目】某校举行了全体学生的一分钟跳绳比赛,为了了解学生的体质,随机抽取了100名学生,其跳绳个数的频数分布表如下:
一分钟跳绳个数 |
|
|
|
|
|
|
|
频数 | 6 | 12 | 18 | 30 | 16 | 10 | 8 |
(1)若将抽取的100名学生一分钟跳绳个数作为一个样本,请将这100名学生一分钟跳绳个数的频率分布直方图补充完整(只画图,不需要写出计算过程);
(2)若该校共有3000名学生,所有学生的一分钟跳绳个数X近似服从正态分布![]() ,其中
,其中![]() 为样本平均数的估计值(同一组中的数据用该组区间的中点值为代表).利用所得正态分布模型,解决以下问题:
为样本平均数的估计值(同一组中的数据用该组区间的中点值为代表).利用所得正态分布模型,解决以下问题:
①估计该校一分钟跳绳个数超过165个的人数(结果四舍五入到整数);
②若在该校所有学生中任意抽取4人,设一分钟跳绳个数超过180个的人数为![]() ,求随机变量
,求随机变量![]() 的分布列、期望与方差./span>
的分布列、期望与方差./span>
附:若随机变量Z服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+1|﹣|2x﹣2|的最大值为M,正实数a,b满足a+b=M.
(1)求2a2+b2的最小值;
(2)求证:aabb≥ab.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线E:y2=2px(p>0)的焦点为F,以F为圆心,3p为半径的圆交抛物线E于P,Q两点,以线段PF为直径的圆经过点(0,﹣1),则点F到直线PQ的距离为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机调查某城市80名有子女在读小学的成年人,以研究晚上八点至十点时间段辅导子女作业与性别的关系,得到下面的数据表:
是否辅导 性别 | 辅导 | 不辅导 | 合计 |
男 | 25 | 60 | |
女 | |||
合计 | 40 | 80 |
(1)请将表中数据补充完整;
(2)用样本的频率估计总体的概率,估计这个城市有子女在读小学的成人女性晚上八点至十点辅导子女作业的概率;
(3)根据以上数据,能否有99%以上的把握认为“晚上八点至十点时间段是否辅导子女作业与性别有关?”.
参考公式: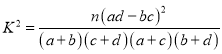 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了防止受到核污染的产品影响我国民众的身体健康,要求产品在进入市场前必须进行两轮核辐射检测,只有两轮都合格才能进行销售,否则不能销售.已知某产品第一轮检测不合格的概率为![]() ,第二轮检测不合格的概率为
,第二轮检测不合格的概率为![]() ,两轮检测是否合格相互没有影响.若产品可以销售,则每件产品获利40元;若产品不能销售,则每件产品亏损80元.已知一箱中有4件产品,记一箱产品获利X元,则P(X≥-80)=________.
,两轮检测是否合格相互没有影响.若产品可以销售,则每件产品获利40元;若产品不能销售,则每件产品亏损80元.已知一箱中有4件产品,记一箱产品获利X元,则P(X≥-80)=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com