
【题目】已知函数![]() .
.
(1)若函数![]() 是奇函数,求实数
是奇函数,求实数![]() 的值;
的值;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有解,求实数
上有解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)求出函数![]() 的解析式,由奇函数的定义得出
的解析式,由奇函数的定义得出![]() ,结合指数运算可求出实数
,结合指数运算可求出实数![]() 的值;
的值;
(2)由(1)知,函数![]() 为奇函数且为减函数,由
为奇函数且为减函数,由![]() ,得出
,得出![]() ,可得出关于
,可得出关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有解,构造函数
上有解,构造函数![]() ,将问题转化为二次函数
,将问题转化为二次函数![]() 在区间
在区间![]() 上有零点,结合二次函数零点分布求出实数
上有零点,结合二次函数零点分布求出实数![]() 的取值范围.
的取值范围.
(1)![]() ,函数
,函数![]() 的定义域为
的定义域为![]() ,
,
由于函数![]() 是奇函数,则
是奇函数,则![]() ,即
,即![]() ,
,
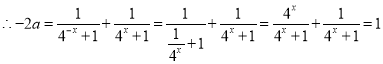 ,因此,
,因此,![]() ;
;
(2)![]() 是奇函数,
是奇函数,
则方程![]() 等价为
等价为
![]() ,即
,即![]() ,
,
则![]() ,
,
![]() 函数
函数![]() 在定义域上是单调函数,
在定义域上是单调函数,![]() 在区间
在区间![]() 上有解,
上有解,
即![]() 在区间
在区间![]() 上有解.
上有解.
构造函数![]() ,
,![]() .
.
①若函数![]() 在区间
在区间![]() 有且只有一个零点,
有且只有一个零点,
则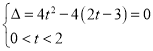 或
或![]() ,解得
,解得![]() 或
或![]() .
.
当![]() 时,
时,![]() ,令
,令![]() ,得
,得![]() ,
,![]() ,不合乎题意;
,不合乎题意;
当![]() 时,
时,![]() ,令
,令![]() ,得
,得![]() ,
,![]() ,不合乎题意;
,不合乎题意;
②若函数![]() 在区间
在区间![]() 有两个零点,则
有两个零点,则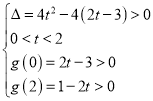 ,此时
,此时![]() .
.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,抛掷一蓝、一黄两枚质地均匀的正四面体骰子,分别观察底面上的数字.

(1)用表格表示试验的所有可能结果;
(2)列举下列事件包含的样本点:A=“两个数字相同”,B=“两个数字之和等于5”,C=“蓝色骰子的数字为2”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某颜料公司生产A,B两种产品,其中生产每吨A产品,需要甲染料1吨,乙染料4吨,丙染料2吨,生产每吨B产品,需要甲染料1吨,乙染料0吨,丙染料5吨,且该公司一天之内甲、乙、丙三种染料的用量分别不超过50吨,160吨和200吨,如果A产品的利润为300元/吨,B产品的利润为200元/吨,设公司计划一天内安排生产A产品x吨,B产品y吨.
(I)用x,y列出满足条件的数学关系式,并在下面的坐标系中画出相应的平面区域;
(II)该公司每天需生产A,B产品各多少吨可获得最大利润,最大利润是多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知函数y=4cos2x-4![]() sinxcosx-1(x∈R).
sinxcosx-1(x∈R).
(1)求出函数的最小正周期;
(2)求出函数的最大值及其相对应的x值;
(3)求出函数的单调增区间;
(4)求出函数的对称轴.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足条件f(0)=1,及f(x+1)﹣f(x)=2x.
(1)求函数f(x)的解析式;
(2)在区间[﹣1,1]上,y=f(x)的图象恒在y=2x+m的图象上方,试确定实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若某校研究性学习小组共6人,计划同时参观科普展,该科普展共有甲,乙,丙三个展厅,6人各自随机地确定参观顺序,在每个展厅参观一小时后去其他展厅,所有展厅参观结束后集合返回,设事件A为:在参观的第一小时时间内,甲,乙,丙三个展厅恰好分别有该小组的2个人;事件B为:在参观的第二个小时时间内,该小组在甲展厅人数恰好为2人,则![]() ( ).
( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com