函数f(x)=-x2+4x-1在[t,t+1]上的最大值为g(t),则g(t)的最大值为 ________.
3
分析:因为对称轴固定,区间不固定,须分轴在区间左边,轴在区间右边,轴在区间中间三种情况讨论,找出g(t)的表达式,再求其最大值.
解答:因为f(x)=-x
2+4x-1开口向下,对称轴为x=2,所以须分以下三种情况讨论
①轴在区间右边,t+1≤2?t≤1,f(x)=-x
2+4x-1在[t,t+1]上的最大值为f(t)=-t
2+4t-1.
故g(t)=-t
2+4t-1.
②轴在区间中间,t<2<t+1?1<t<2,f(x)=-x
2+4x-1在[t,t+1]上的最大值为f(2)=-2
2+4×2-1=3.
故g(t)=3.
③轴在区间左边,t≥2,f(x)=-x
2+4x-1在[t,t+1]上的最大值为f(t)=-t
2+2t+2.
故g(t)=-t
2+2t+2.
∴g(t)=
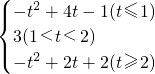
,
∴g(t)的最大值为3
故答案为;3
点评:本题的实质是求二次函数的最值问题,关于给定解析式的二次函数在不固定闭区间上的最值问题,一般是根据对称轴和闭区间的位置关系来进行分类讨论,如轴在区间左边,,轴在区间右边,轴在区间中间,最后在综合归纳得出所需结论

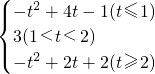 ,
,

 习题精选系列答案
习题精选系列答案