
【题目】在如图所示的几何体中,四边形![]() 是菱形,
是菱形,![]() 是矩形,
是矩形,![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() 为
为![]() 的中点.
的中点.

(1)平面![]() 平面
平面![]()
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.
【答案】(1)见解析;(2)![]()
【解析】
(1)由四边形![]() 为矩形,所以
为矩形,所以![]() ,再由勾股定理,得到
,再由勾股定理,得到![]() ,利用线面垂直的判定定理,证得
,利用线面垂直的判定定理,证得![]() 平面
平面![]() ,进而得到平面
,进而得到平面![]() 平面
平面![]() .
.
(2)建立空间直角坐标系![]() ,求得平面
,求得平面![]() 的法向量为
的法向量为![]() ,又由平面
,又由平面![]() 的法向量
的法向量![]() ,利用向量的夹角公式,即可求解,得到结论.
,利用向量的夹角公式,即可求解,得到结论.
(1)证明:由题意知,四边形![]() 为矩形,所以
为矩形,所以![]() ,
,
又∵四边形![]() 为菱形,
为菱形,![]() 为
为![]() 中点,
中点,
所以![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]()
(2)假设线段![]() 上存在点
上存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ,在
,在![]() 上取一点
上取一点![]() ,
,
连接![]() ,
,![]() .
.
由于四边形![]() 是菱形,且
是菱形,且![]() ,
,![]() 是
是![]() 的中点,可得
的中点,可得![]() .
.
又四边形![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
所以建立如图所示的空间直角坐标系![]()
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,
,
则 ,∴
,∴![]() ,令
,令![]() ,则
,则![]() ,
,
又平面![]() 的法向量
的法向量![]() ,
,
所以 ,解得
,解得![]() ,
,
所以在线段![]() 上存在点
上存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ,此时
,此时![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+m|+|2x-1|.
(1)当m=-1时,求不等式f(x)≤2的解集;
(2)若f(x)≤|2x+1|的解集包含![]() ,求m的取值范围.
,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,CM,CN为某公园景观湖胖的两条木栈道,∠MCN=120°,现拟在两条木栈道的A,B处设置观景台,记BC=a,AC=b,AB=c(单位:百米)

(1)若a,b,c成等差数列,且公差为4,求b的值;
(2)已知AB=12,记∠ABC=θ,试用θ表示观景路线A-C-B的长,并求观景路线A-C-B长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆锥的顶点为S,底面圆O的两条直径分别为AB和CD,且AB⊥CD,若平面![]() 平面
平面![]() .现有以下四个结论:
.现有以下四个结论:
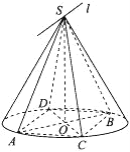
①AD∥平面SBC;
②![]() ;
;
③若E是底面圆周上的动点,则△SAE的最大面积等于△SAB的面积;
④![]() 与平面SCD所成的角为45°.
与平面SCD所成的角为45°.
其中正确结论的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点 ![]() ,且离心率为
,且离心率为![]() .设
.设![]() 为椭圆
为椭圆![]() 的左、右顶点,P为椭圆上异于
的左、右顶点,P为椭圆上异于![]() 的一点,直线
的一点,直线![]() 分别与直线
分别与直线![]() 相交于
相交于![]() 两点,且直线
两点,且直线![]() 与椭圆
与椭圆![]() 交于另一点
交于另一点![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)求证:直线![]() 与
与![]() 的斜率之积为定值;
的斜率之积为定值;
(Ⅲ)判断三点![]() 是否共线,并证明你的结论.
是否共线,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com