练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数f（x）=lnx﹣x3与g（x）=x3﹣ax的图象上存在关于x轴的对称点，则实数a的取值范围为（ ）
    A.（﹣∞，e）
    B.（﹣∞，e]
    C.
    D.

    【答案】D
    【解析】解：函数f（x）=lnx﹣x3与g（x）=x3﹣ax的图象上存在关于x轴的对称点， ∴f（x）=﹣g（x）有解，
    ∴lnx﹣x3=﹣x3+ax，
    ∴lnx=ax，在（0，+∞）有解，
    分别设y=lnx，y=ax，
    若y=ax为y=lnx的切线，
    ∴y′= ，
    设切点为（x0 ， y0），
    ∴a= ，ax0=lnx0 ，
    ∴x0=e，
    ∴a= ，
    结合图象可知，a≤
    故选：D．

    由题意可知f（x）=﹣g（x）有解，即y=lnx与y=ax有交点，根据导数的几何意义，求出切点，结合图象，可知a的范围．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)=x|x-4| (x∈R)

    (1)用分段形式写出函数f(x)的表达式，并作出函数f(x)的图象;

    (2) 根据图象指出f(x)的单调区间,并写出不等式f(x)>0的解集;

    (3) 若h(x)=f(x)-k有三个零点,写出k的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示的几何体ABCDE中，DA⊥平面EAB，CB∥DA，EA=DA=AB=2CB，EA⊥ AB，M是EC上的点（不与端点重合），F为DA上的点，N为BE的中点．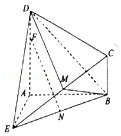

    （Ⅰ）若M是EC的中点，AF=3FD，求证：FN∥平面MBD；
    （Ⅱ）若平面MBD与平面ABD所成角（锐角）的余弦值为 ，试确定点M在EC上的位置．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= ﹣m（lnx+ ）（m为实数，e=2.71828…是自然对数的底数）． （Ⅰ）当m＞1时，讨论f（x）的单调性；
    （Ⅱ）若g（x）=x2f′（x）﹣xex在（ ，3）内有两个零点，求实数m的取值范围．
    （Ⅲ）当m=1时，证明：xf（x）+xlnx+1＞x+ ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设，，若对任意成立，则下列命题中正确的命题个数是（ ）

    （1）

    （2）

    （3）不具有奇偶性

    （4）的单调增区间是

    （5）可能存在经过点的直线与函数的图象不相交

    A. 1个B. 2个C. 3个D. 4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知三点，，，曲线上任意一点满足．

    求的方程；

    已知点，动点 在曲线C上，曲线C在Q处的切线与直线PA,PB都相交，交点分别为D,E，求与的面积的比值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f（x）=Acos（ωx+φ）（A＞0，ω＞0，﹣π＜φ＜0）的部分图象如图所示，为了得到g（x）=Acosωx的图象，只需将函数y=f（x）的图象（ ）
    A.向左平移 个单位长度
    B.向左平移 个单位长度
    C.向右平移 个单位长度
    D.向右平移 个单位长度

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平行四边形ABCD中， ， ，若将其沿AC折成直二面角D﹣AC﹣B，则三棱锥D﹣ACB的外接球的表面积为（ ）
    A.16π
    B.8π
    C.4π
    D.2π

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，将一矩形花坛扩建成一个更大的矩形花坛，要求点在上，点在上，且对角线过点，已知米，米．

    （1）要使矩形的面积大于平方米，则的长应在什么范围内?

    （2）当的长度是多少时，矩形花坛的面积最小?并求出最小值．

    查看答案和解析>>

    同步练习册答案