【题目】甲、乙、丙三名大学生参加学校组织的“国学达人”挑战赛， 每人均有两轮答题机会，当且仅当第一轮不过关时进行第二轮答题.根据平时经验，甲、乙、丙三名大学生每轮过关的概率分别为
，且三名大学生每轮过关与否互不影响.
（1）求甲、乙、丙三名大学生都不过关的概率；
（2）记
为甲、乙、丙三名大学生中过关的人数，求随机变量的分布列和数学期望.
【答案】（1）
（2）见解析
【解析】分析：（1）设事件A表示“甲过关”，事件B表示“乙过关”，事件C表示“丙过关”则
，
，
，由此利用相互独立事件概率乘法公式能求出甲、乙、丙三名大学生都过的概率.
（2）由题意得
的可能取值为
，分别求出相应的概率，由此能求出X的分布列和数学期望.
详解：解：（1）∵甲、乙、丙三名大学生参加学校组织的“国学达人”挑战赛，
每人均有两轮答题机会，当且仅当第一轮不过关时进行第二轮答题.
甲、乙、丙三名大学生每轮过关的概率分别为
，且三名大学生每轮过关与否互不影响.
∴甲过关的概率，
乙关的概率，
丙过关的概率，
∴甲、乙、丙三名大学生都不过关的概率：
.
（2）记为甲、乙、丙二名大学生中过关的人数，则的可能取值为
∴随机变量的分布列为：
数学期望
.
科目：高中数学 来源： 题型：
【题目】已知椭圆
的长轴长为4，直线
被椭圆
截得的线段长为
.
（1）求椭圆的标准方程；
（2）过椭圆的右顶点作互相垂直的两条直线
分别交椭圆于
两点（点不同于椭圆的右顶点），证明：直线
过定点
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知等差数列{an}的公差为2，前n项和为Sn ， 且S1 ， S2 ， S4成等比数列．
（1）求数列{an}的通项公式；
（2）令bn=（﹣1）n﹣1 
，求数列{bn}的前n项和Tn ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】将函数y=3sin（2x+ 
）的图象向右平移 
个单位长度，所得图象对应的函数（ ）
A.在区间[ 
， 
]上单调递减
B.在区间[ ， ]上单调递增
C.在区间[﹣ 
， ]上单调递减
D.在区间[﹣ ， ]上单调递增
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在△ABC中，内角A、B、C的对边分别为a，b，c，且a＞c，已知 
=2，cosB= 
，b=3，求：
（1）a和c的值；
（2）cos（B﹣C）的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
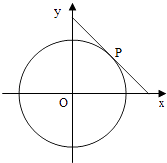
【题目】圆x2+y2=4的切线与x轴正半轴，y轴正半轴围成一个三角形，当该三角形面积最小时，切点为P（如图），双曲线C1： 
过点P且离心率为 
． 
（1）求C1的方程；
（2）若椭圆C2过点P且与C1有相同的焦点，直线l过C2的右焦点且与C2交于A，B两点，若以线段AB为直径的圆过点P，求l的方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】教材上一例问题如下：
一只红铃虫的产卵数y和温度x有关，现收集了7组观测数据如下表，试建立y与x之间的回归方程．
温度 x/℃ | 21 | 23 | 25 | 27 | 29 | 32 | 35 |
产卵数y/个 | 7 | 11 | 21 | 24 | 66 | 115 | 325 |
某同学利用图形计算器研究它时，先作出散点图（如图所示），发现两个变量不呈线性相关关系． 根据已有的函数知识，发现样本点分布在某一条指数型曲线
的附近（
和
是待定的参数），于是进行了如下的计算：
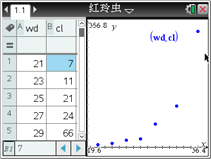
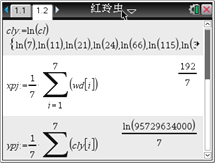
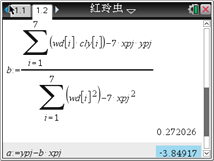
根据以上计算结果，可以得到红铃虫的产卵数y对温度x的回归方程为__________．（精确到0.0001） （提示：利用代换可转化为线性关系）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四棱柱ABCD﹣A1B1C1D1的所有棱长都相等，AC∩BD=O，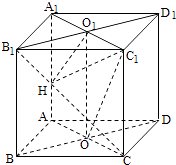 
A1C1∩B1D1=O1 ， 四边形ACC1A1和四边形BDD1B1均为矩形．
（1）证明：O1O⊥底面ABCD；
（2）若∠CBA=60°，求二面角C1﹣OB1﹣D的余弦值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
