Question

已知一个几何体是由上下两部分构成的组合体，其三视图如下，若图中圆的半径为，等腰三角形的腰长为，则该几何体的体积是  （    ）

A．

B．

C．

D．

Answer 1

A

解析试题分析：
由三视图知，此组合体上部是一个圆锥，下部是一个半球，半球体积易求，欲求圆锥体积需先求圆锥的高，再由公式求体积，最后再想加求出组合体的体积。此几何体上部为一圆锥，下部是一个半球，,由于半球的半径为1，故其体积为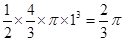,圆锥的高为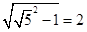，故此圆锥的体积为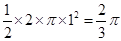
此几何体的体积是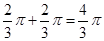故选A
考点：三视图求几何体的面积、体积
点评：本题考点是由三视图求几何体的面积、体积，考查对三视图的理解与应用，主要考查三视图与实物图之间的关系，用三视图中的数据还原出实物图的数据，再根据相关的公式求表面积与体积，本题求的是组合体的体积．三视图的投影规则是：“主视、俯视 长对正；主视、左视高平齐，左视、俯视 宽相等”．三视图是高考的新增考点，不时出现在高考试题中，应予以重视