Question

【题目】已知函数f(x)是定义在R上的奇函数，且当x≥0时，f(x)＝.

(1)求f(x)的解析式；

(2)判断f(x)的单调性；

(3)若对任意的t∈R，不等式f(k－3t2)＋f(t2＋2t)≤0恒成立，求k的取值范围.

Answer 1

【答案】（1）f(x)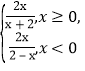＝；(2) f(x)在(－∞，＋∞)上是增函数； （3）k≤－.

【解析】

（1）当x<0时，f(x)＝－f(－x)＝－＝.即得f(x)的解析式. (2)先分析得到 f(x)在[0，＋∞)上是增函数.又f(x)是奇函数，所以f(x)在(－∞，＋∞)上是增函数.（3）利用函数的奇偶性和单调性得到k－3t2≤－t2－2t，即2t2－2t－k≥0，解Δ＝4＋8k≤0，即得解.

(1)因为当x≥0时，f(x)＝，

所以当x<0时，f(x)＝－f(－x)＝－＝.

所以f(x)＝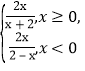

(2)当x≥0时，f(x)＝＝2－，

所以f(x)在[0，＋∞)上是增函数.

又f(x)是奇函数，所以f(x)在(－∞，＋∞)上是增函数.

(3)由题知不等式f(k－3t2)＋f(t2＋2t)≤0等价于

f(k－3t2)≤f(－t2－2t)，

又f(x)在(－∞，＋∞)上是增函数，

所以k－3t2≤－t2－2t，即2t2－2t－k≥0，

即对一切t∈R，恒有2t2－2t－k≥0，

所以Δ＝4＋8k≤0，解得k≤－.