
| A. | 4 | B. | 4 | C. | 12 | D. | 16 |
分析 ∵a>0,b>0,∴不等式$\frac{mab}{3a+b}≤a+3b$恒成立⇒m≤$\frac{(3a+b)(a+3b)}{ab}=\frac{10ab+3{a}^{2}+3{b}^{2}}{ab}$=10+$\frac{3{a}^{2}+3{b}^{2}}{ab}$,求出=10+$\frac{3{a}^{2}+3{b}^{2}}{ab}$的最小值即可.
解答 解:∵a>0,b>0,∴不等式$\frac{mab}{3a+b}≤a+3b$恒成立⇒m≤$\frac{(3a+b)(a+3b)}{ab}=\frac{10ab+3{a}^{2}+3{b}^{2}}{ab}$=10+$\frac{3{a}^{2}+3{b}^{2}}{ab}$,∵10+$\frac{3{a}^{2}+3{b}^{2}}{ab}≥10+\frac{2\sqrt{9{a}^{2}{b}^{2}}}{ab}=16$,∴m≤16,故选:D
点评 本题主要考查基本不等式的应用,函数的恒成立问题,属于基础题.


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:选择题
| A. | f(x)=4x3+x | B. | $f(x)=ln\frac{5-x}{5+x}$ | C. | $f(x)=tan\frac{x}{2}$ | D. | f(x)=ex+e-x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{7}{2}$ | C. | 4 | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{a=-1}\\{b=0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=1}\\{b=0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=0}\\{b=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=0}\\{b=-1}\end{array}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | (-∞,-2)∪(1,+∞) | B. | (-∞,-2)∪(1,2) | C. | (-∞,-1)∪(-1,1)∪(3,+∞) | D. | (-∞,-1)∪(-1,0)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
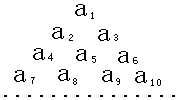 已知数列{an}是首项为1,公差为2的等差数列,将数列{an}中的各项排成如图所示的一个三角形数表,记A(i,j)表示第i行从左至右的第j个数,例如A(4,3)=a9,则A(10,2)=93.
已知数列{an}是首项为1,公差为2的等差数列,将数列{an}中的各项排成如图所示的一个三角形数表,记A(i,j)表示第i行从左至右的第j个数,例如A(4,3)=a9,则A(10,2)=93.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 72.705尺 | B. | 61.395尺 | C. | 61.905尺 | D. | 73.995尺 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com