
 中,角A,B,C的对边分别是
中,角A,B,C的对边分别是 且满足
且满足
 的面积为为
的面积为为 且
且 ,求
,求 的值;
的值; . ⑵a+c=
. ⑵a+c= .
. ,又0<B<π,则
,又0<B<π,则 ;
; ,sinB=sin
,sinB=sin =
= ,
, acsinB=
acsinB=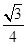 ac=
ac= ,
, ,cosB=cos
,cosB=cos =
= ,
, .
.

科目:高中数学 来源:不详 题型:单选题
 ,则线段AM的长度是( )
,则线段AM的长度是( )A. | B. | C.5 | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
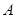 北偏东
北偏东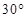 方向的点
方向的点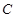 处有一观测站,港口正东方向的
处有一观测站,港口正东方向的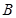 处有一轮船,测得
处有一轮船,测得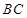 为
为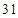 海里.该轮船从
海里.该轮船从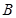 处沿正西方向航行
处沿正西方向航行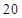 海里后到达
海里后到达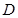 处,测得
处,测得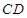 为
为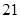 海里. 问此时轮船离港口
海里. 问此时轮船离港口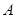 还有多少海里?
还有多少海里?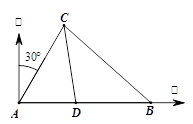
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ,爬行10 cm捕捉到另一只小虫,这时它向右转
,爬行10 cm捕捉到另一只小虫,这时它向右转 爬行回它的出发点,那么x=_______.
爬行回它的出发点,那么x=_______.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com