
【题目】已知菱形 ABCD 中,对角线 AC 与 BD 相交于一点 O,∠A=60°,将△BDC 沿着 BD 折起得△BDC',连结 AC'.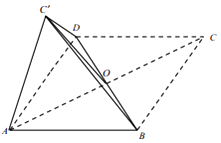
(Ⅰ)求证:平面 AOC'⊥平面 ABD;
(Ⅱ)若点 C'在平面 ABD 上的投影恰好是△ABD 的重心,求直线 CD 与底面 ADC'所成角的正弦值.
【答案】解:(Ⅰ)∵C′O⊥DB,AO⊥BD,C′O∩AO=O,∴BD⊥面 AOC',
又BD平面 ABD,∴平面 AOC'⊥平面 ABD.
(Ⅱ)如图建立空间直角坐标系O﹣xyz,

令AB=a,则A( ![]() ,0,0).
,0,0).
B(0, ![]() ,0),D(0,﹣
,0),D(0,﹣ ![]() ,0),C′(
,0),C′( ![]() ),
),
设面ADC'的法向量为 ![]()
![]() ,
, ![]() ,
, ![]()
由  可取
可取 ![]()
![]()
∴直线 CD 与底面 ADC'所成角的正弦值为: ![]()
【解析】(Ⅰ)只需证明C′O⊥DB,AO⊥BD,C′O∩AO=O,BD⊥面 AOC',即可得平面 AOC'⊥平面 ABD;
(Ⅱ)如图建立空间直角坐标系O﹣xyz,令AB=a,则A(![]() ,0,0),B(0,
,0,0),B(0,![]() ,0),D(0,﹣
,0),D(0,﹣ ![]() ,0),C′(
,0),C′( ![]() , 0 ,
, 0 ,![]() ),利用向量法求解。
),利用向量法求解。
【考点精析】根据题目的已知条件,利用平面与平面垂直的判定和空间角的异面直线所成的角的相关知识可以得到问题的答案,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 .
.


科目:高中数学 来源: 题型:
【题目】某港口水的深度y(m)是时间t(0≤t≤24,单位:h)的函数,记作y=f(t).下面是某日水深的数据:
t/h | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y/m | 10 | 13 | 10 | 7 | 10 | 13 | 10 | 7 | 10 |
经长期观察,y=f(t)的曲线可以近似地看成函数![]() 的图象.一般情况下,船舶航行时,船底离海底的距离为5m或5m以上时认为是安全的(船舶停靠时,船底只需不碰海底即可).
的图象.一般情况下,船舶航行时,船底离海底的距离为5m或5m以上时认为是安全的(船舶停靠时,船底只需不碰海底即可).
(1)求y与t满足的函数关系式;
(2)某船吃水深度(船底离水面的距离)为6.5m,如果该船希望在同—天内安全进出港,请问该船在什么时间段能够安全进港?它同一天内最多能在港内停留多少小时?(忽略进 出港所需的时间).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋内装有6个球,每个球上都记有从1到6的一个号码,设号码为n的球重![]() 克,这些球等可能地从袋里取出(不受重量、号码的影响).
克,这些球等可能地从袋里取出(不受重量、号码的影响).
(1)如果任意取出1个球,求其重量大于号码数的概率;
(2)如果不放回地任意取出2个球,求它们重量相等的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小王、小张两位同学玩投掷正四面体(每个面都为等边三角形的正三棱锥)骰子(骰子质地均匀,各面上的点数分别为![]() )游戏,规则:小王现掷一枚骰子,向下的点数记为
)游戏,规则:小王现掷一枚骰子,向下的点数记为![]() ,小张后掷一枚骰子,向下的点数记为
,小张后掷一枚骰子,向下的点数记为![]() ,
,
(1)在直角坐标系![]() 中,以
中,以![]() 为坐标的点共有几个?试求点
为坐标的点共有几个?试求点![]() 落在直线
落在直线![]() 上的概率;
上的概率;
(2)规定:若![]() ,则小王赢,若
,则小王赢,若![]() ,则小张赢,其他情况不分输赢,试问这个游戏公平吗?请说明理由.
,则小张赢,其他情况不分输赢,试问这个游戏公平吗?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的外接圆半径为1,角A,B,C的对边分别为a,b,c,且2acos A=ccos B+bcos C.
(Ⅰ)求A;
(Ⅱ)若b2+c2=7,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() ,g(x)=a(x+b)(0<a≤1,b≤0).
,g(x)=a(x+b)(0<a≤1,b≤0).
(1)讨论函数y=f(x)g(x)的奇偶性;
(2)当b=0时,判断函数y= ![]() 在(﹣1,1)上的单调性,并说明理由;
在(﹣1,1)上的单调性,并说明理由;
(3)设h(x)=|af2(x)﹣ ![]() |,若h(x)的最大值为2,求a+b的取值范围.
|,若h(x)的最大值为2,求a+b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆E: ![]() (a>b>0)过点(
(a>b>0)过点( ![]() ,1),且与直线
,1),且与直线 ![]() x+2y﹣4=0相切.
x+2y﹣4=0相切.
(1)求椭圆E的方程;
(2)若椭圆E与x轴交于M、N两点,椭圆E内部的动点P使|PM|、|PO|、|PN|成等比数列,求 ![]()
![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com