
分析 (I)由题意可知:|F1F2|=2c=2,则c=1,2|F1F2|=|PF1|+|PF2|=2a,则a=2,b2=a2-c2=3,即可写出椭圆的方程;
(II)设直线m方程为x=ty+1,代入椭圆方程,由韦达定理及向量数量积的坐标运算,即可求得t的值,求得直线m的斜率.
解答 解:(I)由题意设椭圆的方程:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),
由|F1F2|=2c=2,则c=1,
|PF1|、|F1F2|、|PF2|构成等差数列.即2|F1F2|=|PF1|+|PF2|=2a,则a=2,
b2=a2-c2=3,
椭圆C的方程$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;…(5分)
( II)由题意知直线m的斜率不为0,且经过右焦点(1,0),故设直线m方程为x=ty+1
代入$\frac{x^2}{4}+\frac{y^2}{3}=1$,得(3t2+4)y2+6yt-9=0
显然△>0,设P(x1,y1),Q(x2,y2)$则{y_1}+{y_2}=-\frac{6t}{{3{t^2}+4}}$…①${y_1}{y_2}=\frac{-9}{{3{t^2}+4}}$…②
由${\overrightarrow{QF}_2}=2\overrightarrow{{F_2}P}$,得y2=-2y1…③
解①②③得$t=±\frac{2}{{\sqrt{5}}}$,
所以,直线m的斜率$k=\frac{1}{t}=±\frac{{\sqrt{5}}}{2}$…(12分)
点评 本题考查椭圆的标准方程及简单几何性质,考查直线与椭圆的位置关系,韦达定理,向量数量积的坐标运算,考查计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
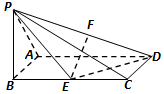 如图,已知PB⊥矩形ABCD所在的平面,E,F分别是BC,PD的中点,∠PAB=45°,AB=1,BC=2.
如图,已知PB⊥矩形ABCD所在的平面,E,F分别是BC,PD的中点,∠PAB=45°,AB=1,BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
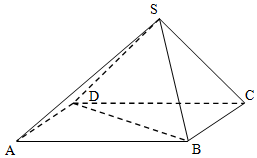 如图所示,在四棱锥S-ABCD中,底面ABCD是矩形,侧面SDC⊥底面ABCD,且AB=2,SC=SD=$\sqrt{2}$.
如图所示,在四棱锥S-ABCD中,底面ABCD是矩形,侧面SDC⊥底面ABCD,且AB=2,SC=SD=$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com