
【题目】对于函数y=f(x),若在其定义域内存在x0,使得x0f(x0)=1成立,则称函数f(x)具有性质M.
(1)下列函数中具有性质M的有____
①f(x)=﹣x+2
②f(x)=sinx(x∈[0,2π])
③f(x)=x![]() ,(x∈(0,+∞))
,(x∈(0,+∞))
④f(x)![]()
(2)若函数f(x)=a(|x﹣2|﹣1)(x∈[﹣1,+∞))具有性质M,则实数a的取值范围是____.
【答案】①②④ a![]() 或a>0
或a>0
【解析】
(1)①因为f(x)=﹣x+2,若存在,则![]() ,解一元二次方程即可.②若存在,则
,解一元二次方程即可.②若存在,则![]() ,即
,即![]() ,再利用零点存在定理判断.③若存在,则
,再利用零点存在定理判断.③若存在,则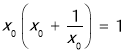 ,直接解方程.④若存在,则
,直接解方程.④若存在,则![]() ,即
,即![]() ,令
,令![]() ,再利用零点存在定理判断.
,再利用零点存在定理判断.
(2)若函数f(x)=a(|x﹣2|﹣1)(x∈[﹣1,+∞))具有性质M,则ax(|x﹣2|﹣1)=1,x∈[﹣1,+∞)有解,将问题转化 :当![]() 时,
时,![]() 有解,当
有解,当![]() 时,
时,![]() 有解,分别用二次函数的性质求解.
有解,分别用二次函数的性质求解.
(1)①因为f(x)=﹣x+2,若存在,则![]() ,
,
即![]() ,所以
,所以![]() ,存在.
,存在.
②因为f(x)=sinx(x∈[0,2π]),若存在,则![]() ,
,
即![]() ,
,
令![]() ,
,
因为![]() ,
,
所以存在![]() .
.
③因为f(x)=x![]() ,(x∈(0,/span>+∞)),若存在,则
,(x∈(0,/span>+∞)),若存在,则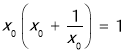 ,
,
即![]() ,所以不存在.
,所以不存在.
④因为f(x)![]() ,(x∈(0,+∞)),若存在,则
,(x∈(0,+∞)),若存在,则![]() ,
,
即![]() ,
,
令![]() ,
,
因为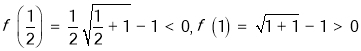 ,
,
所以存在![]() .
.
(2)若函数f(x)=a(|x﹣2|﹣1)(x∈[﹣1,+∞))具有性质M,
则ax(|x﹣2|﹣1)=1,x∈[﹣1,+∞)有解,
当![]() 时,
时,![]() 有解,
有解,
令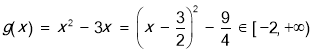 ,
,
所以![]() .
.
当![]() 时,
时,![]() 有解,
有解,
令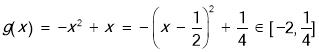 ,
,
所以![]() .
.
综上:实数a的取值范围是a![]() 或a>0.
或a>0.
故答案为:(1). ①②④ (2). a![]() 或a>0
或a>0


科目:高中数学 来源: 题型:
【题目】某课题小组共10人,已知该小组外出参加交流活动次数为1,2,3的人数分别为3,3, 4,现从这10人中随机选出2人作为该组代表参加座谈会.
(1)记“选出2人外出参加交流活动次数之和为4”为事件A,求事件A发生的概率;
(2)设X为选出2人参加交流活动次数之差的绝对值,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点F与抛物线
的右焦点F与抛物线![]() 焦点重合,且椭圆的离心率为
焦点重合,且椭圆的离心率为![]() ,过
,过![]() 轴正半轴一点
轴正半轴一点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点.
两点.
(1)求椭圆的标准方程;
(2)是否存在实数![]() 使以线段
使以线段![]() 为直径的圆经过点
为直径的圆经过点![]() ,若存在,求出实数
,若存在,求出实数![]() 的值;若不存在说明理由.
的值;若不存在说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.

(Ⅰ)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,并说明理由;
,并说明理由;
(Ⅱ)当二面角![]() 的余弦值为
的余弦值为![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成的角.
所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知角α的顶点与原点O重合,始边与x轴的非负半轴重合,它的终边上有一点P的坐标是(3a,a),其中a≠0.
(1)求cos(α![]() )的值;
)的值;
(2)若tan(2α+β)=1,求tanβ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f1(x),y=f2(x),定义函数f(x) .
.
(1)设函数f1(x)=x+3,f2(x)=x2﹣x,求函数y=f(x)的解析式;
(2)在(1)的条件下,g(x)=mx+2(m∈R),函数h(x)=f(x)﹣g(x)有三个不同的零点,求实数m的取值范围;
(3)设函数f1(x)=x2﹣2,f2(x)=|x﹣a|,函数F(x)=f1(x)+f2(x),求函数F(x)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有甲,乙,丙,丁四位同学课余参加巴蜀爱心社和巴蜀文学风的活动,每人参加且只能参加一个社团的活动,并且参加每个社团都是等可能的.
(1)求巴蜀爱心社和巴蜀文学风都至少有1人参加的概率;
(2)求甲,乙在同一个社团,丙,丁不在同一个社团的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 分别为内角
分别为内角![]() 所对的边,且满足
所对的边,且满足![]() .
.
(Ⅰ)求![]() 的大小;
的大小;
(Ⅱ)现给出三个条件:①![]() ; ②
; ②![]() ;③
;③![]() .
.
试从中选出两个可以确定![]() 的条件,写出你的选择并以此为依据求
的条件,写出你的选择并以此为依据求![]() 的面积 (只需写出一个选定方案即可,选多种方案以第一种方案记分)
的面积 (只需写出一个选定方案即可,选多种方案以第一种方案记分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com