
(09年丰台区期末理)(13分)
已知向量![]() =
=![]() ,
,![]() =
=![]() ,且x∈
,且x∈![]() 。
。
(Ⅰ)求![]() ?
?![]() 及|
及|![]() ?
?![]() |;
|;
(Ⅱ)若f ( x ) = ![]() ?
?![]()
![]() |
|![]() ?
?![]() |的最小值为
|的最小值为![]() ,且
,且![]() ∈
∈![]() ,求
,求![]() 的值。
的值。
解析:(Ⅰ)![]() ?
?![]() =
=![]() = cos2x ……………………… 2分
= cos2x ……………………… 2分
|![]() +
+![]() | =
| =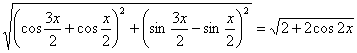 … 5分
… 5分
因为 x∈![]() ,所以 cosx
,所以 cosx![]() 0 所以|
0 所以|![]() +
+![]() | = 2cos x ………… 6分
| = 2cos x ………… 6分
(Ⅱ)f ( x ) =![]() ?
?![]() 2
2![]() |
|![]() +
+![]() | = 2cos x 4
| = 2cos x 4![]() cos x = 2 cos2x 4
cos x = 2 cos2x 4![]() cos x 1
cos x 1
= 2 ( cos x ![]() )2 1 2
)2 1 2![]() 2 ……………………………… 8分
2 ……………………………… 8分
令t = cos x∈[ 0 , 1 ],则f ( x ) = g ( t ) = 2 ( t ![]() )2 1 2
)2 1 2![]() 2
2
①当0![]()
![]()
![]() 1时,当且仅当t =
1时,当且仅当t =![]() 时,f ( x )取得最小值,
时,f ( x )取得最小值,
g (![]() ) = 1 2
) = 1 2![]() 2 即 1 2
2 即 1 2![]() 2兴=
2兴=![]()
![]()
![]() =
=![]() ………… 10分
………… 10分
②当![]() >1时,当且仅当t = 1时,f ( x )取得最小值,g ( 1 ) = 1 4
>1时,当且仅当t = 1时,f ( x )取得最小值,g ( 1 ) = 1 4![]()
即1 4![]()
![]()
![]()
![]() =
=![]() <1不合题意,舍去。……………………… 12分
<1不合题意,舍去。……………………… 12分


科目:高中数学 来源: 题型:
(09年丰台区期末理)(14分)
设椭圆M:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,长轴长为
,长轴长为![]() ,设过右焦点F倾
,设过右焦点F倾
斜角为![]() 的直线交椭圆M于A,B两点。
的直线交椭圆M于A,B两点。
(Ⅰ)求椭圆M的方程;
(Ⅱ)求证| AB | =![]() ;
;
(Ⅲ)设过右焦点F且与直线AB垂直的直线交椭圆M于C,D,求|AB| + |CD|的最小
值。
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年丰台区期末理)(14分)
设椭圆M:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,长轴长为
,长轴长为![]() ,设过右焦点F倾
,设过右焦点F倾
斜角为![]() 的直线交椭圆M于A,B两点。
的直线交椭圆M于A,B两点。
(Ⅰ)求椭圆M的方程;
(Ⅱ)求证| AB | =![]() ;
;
(Ⅲ)设过右焦点F且与直线AB垂直的直线交椭圆M于C,D,求|AB| + |CD|的最小
值。
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年丰台区期末理)(14分)
设椭圆M:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,长轴长为
,长轴长为![]() ,设过右焦点F倾
,设过右焦点F倾
斜角为![]() 的直线交椭圆M于A,B两点。
的直线交椭圆M于A,B两点。
(Ⅰ)求椭圆M的方程;
(Ⅱ)求证| AB | =![]() ;
;
(Ⅲ)设过右焦点F且与直线AB垂直的直线交椭圆M于C,D,求|AB| + |CD|的最小
值。
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年丰台区期末理)(13分)
已知函数f ( x ) = 3x , f ( a + 2 ) = 18 , g ( x ) =![]() ? 3ax 4x的义域为[0,1]。
? 3ax 4x的义域为[0,1]。
(Ⅰ)求a的值;
(Ⅱ)若函数g ( x )在区间[0,1]上是单调递减函数,求实数查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com