
 ,其中t是产品售出的数量,且
,其中t是产品售出的数量,且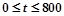 (利润=销售收入
(利润=销售收入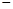 成本).
成本).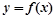 的解析式;
的解析式;科目:高中数学 来源:不详 题型:解答题
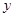 (万元)与处理量
(万元)与处理量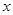 (吨)之间的函数关系可近似地表示为:
(吨)之间的函数关系可近似地表示为: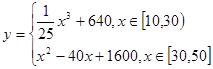 , 且每处理一吨二氧化碳可得价值为
, 且每处理一吨二氧化碳可得价值为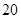 万元的某种化工产品.
万元的某种化工产品. 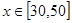 时,判断该技术改进能否获利?如果能获利,求出最大利润;如果不能获利,则国家至少需要补贴多少万元,该工厂才不亏损?
时,判断该技术改进能否获利?如果能获利,求出最大利润;如果不能获利,则国家至少需要补贴多少万元,该工厂才不亏损? 查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.f (x)=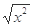 , g(x)=x , g(x)=x | B.f (x)=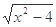 , g(x)= , g(x)=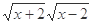 |
C.f (x)=x, g(x)=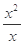 | D.f (x)=|x+1|, g(x)=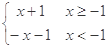 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
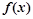 的定义域为D,若存在非零常数l使得对于任意
的定义域为D,若存在非零常数l使得对于任意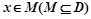 有
有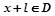 且
且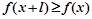 ,则称
,则称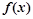 为M上的l高调函数.对于定义域为R的奇函数
为M上的l高调函数.对于定义域为R的奇函数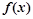 ,当
,当 ,若
,若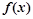 为R上的4高调函数,则实数a的取值范围为________
为R上的4高调函数,则实数a的取值范围为________查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com