
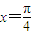 时,函数f(x)=Asin(x+φ)(A>0)取得最小值,则函数
时,函数f(x)=Asin(x+φ)(A>0)取得最小值,则函数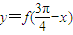 是( )
是( )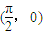 对称
对称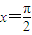 对称
对称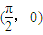 对称
对称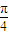 )=sin(
)=sin(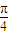 +φ)=-1可求得φ=2kπ-
+φ)=-1可求得φ=2kπ-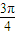 (k∈Z),从而可求得y=f(
(k∈Z),从而可求得y=f(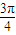 -x)的解析式,利用正弦函数的奇偶性与对称性判断即可.
-x)的解析式,利用正弦函数的奇偶性与对称性判断即可.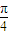 )=sin(
)=sin(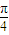 +φ)=-1,
+φ)=-1,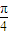 +φ=2kπ-
+φ=2kπ-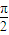 ,
,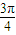 (k∈Z),
(k∈Z),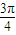 -x)=Asin(
-x)=Asin(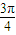 -x+2kπ-
-x+2kπ- )=-Asinx,
)=-Asinx,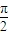 ,k∈Z,对称中心为(kπ,0)k∈Z,可排除A;
,k∈Z,对称中心为(kπ,0)k∈Z,可排除A;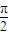 为一条对称轴,
为一条对称轴,

科目:高中数学 来源:2012-2013学年福建省泉州市南安一中高三(上)期中数学复习试卷1(文科)(解析版) 题型:解答题
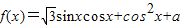 .
. 时,函数f(x)的最大值与最小值的和为
时,函数f(x)的最大值与最小值的和为 ,求a的值.
,求a的值.查看答案和解析>>
科目:高中数学 来源:2009-2010学年广东省揭阳市揭西县河婆中学高三(上)11月月考数学试卷(理科)(解析版) 题型:解答题
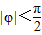 .
.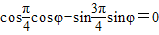 ,求φ的值;
,求φ的值;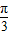 ,求当
,求当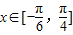 时,函数f(x)的值域.
时,函数f(x)的值域.查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省广州市育才中学高三(上)各类题型综合训练:三角函数(解析版) 题型:解答题
 定义在区间
定义在区间 上的函数y=f(x)的图象关于直线
上的函数y=f(x)的图象关于直线 对称,当
对称,当 时,函数f(x)=Asin(ωx+φ),
时,函数f(x)=Asin(ωx+φ), ,其图象如图.
,其图象如图. 上的表达式;
上的表达式; 的解集.
的解集.查看答案和解析>>
科目:高中数学 来源:2013年河北省衡水市冀州中学高三一轮检测数学试卷(理科)(解析版) 题型:选择题
 时,函数f(x)=Asin(x+φ)(A>0)取得最小值,则函数
时,函数f(x)=Asin(x+φ)(A>0)取得最小值,则函数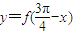 是( )
是( )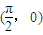 对称
对称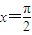 对称
对称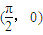 对称
对称查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省桐乡市高三10月月考理科数学 题型:解答题
(本题满分14分)已知 函数
函数
(Ⅰ)求f(x)的最小正周期,并求其图象对称中心的坐标;
(Ⅱ)当 时,求函数f(x)的值域.
时,求函数f(x)的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com