
【题目】如图,正方形ADEF与梯形ABCD所在平面互相垂直,![]() ,
,![]() ,点M是EC的中点.
,点M是EC的中点.
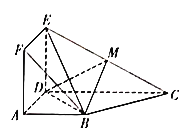
(1)求证:平面ADEF![]() 平面BDE.
平面BDE.
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见证明;(2) ![]()
【解析】
(1)由勾股定理可得BD⊥AD,再利用面面垂直的性质可得ED⊥BD,结论得证;
(2)建立直角坐标系,分别求出平面BDE和平面BDM的法向量,利用空间向量求其二面角可得答案.
解:(1)由题可知AD=BD=2,AB=![]() 则AD2+BD2=AB,
则AD2+BD2=AB,
根据勾股定理有BD⊥AD,
又因正方形ADEF 与梯形ABCD所在平面互相垂直,则ED⊥平面ABCD,
则ED⊥BD,而AD∩ED=D,所以BD⊥平面ADEF.
而BD![]() 平面BDE,所以平面ADEF⊥平面BDE.
平面BDE,所以平面ADEF⊥平面BDE.
(2)以D为坐标原点,分别以DA,DB,DE为x轴,y轴,z轴建立空间直角坐标系,
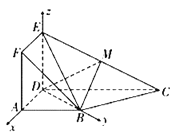
由题可得D(0,0,0),A(2,0,0),B(0.2,0),E(0,0,2),C(-2![]() ,2
,2![]() ,0),M(-
,0),M(-![]() ,
,![]() ,1).
,1).
由(1)可得AD⊥平面BDE,则可取平面BDE的法向量![]() ,设平面BDM的法向量为
,设平面BDM的法向量为![]() ,
,![]() =(-
=(-![]() ,
,![]() ,1),
,1),![]() =(0,2,0),
=(0,2,0),
由![]() ·
·![]() =0,
=0,![]() ·
·![]() =0,.可得
=0,.可得![]()
可取![]() =(
=(![]() ,0,2),则
,0,2),则![]() .
.
设二面角E-BD-M的平面角为α,显然α为锐角,
故![]()


科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,
,![]() 与
与![]() 轴的交点为
轴的交点为![]() ,点
,点![]() 在抛物线
在抛物线![]() 上,过点
上,过点![]() 作
作![]() 于点
于点![]() ,如图1.已知
,如图1.已知![]() ,且四边形
,且四边形![]() 的面积为
的面积为![]() .
.


(1)求抛物线![]() 的方程;
的方程;
(2)若正方形![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() 都在抛物线
都在抛物线![]() 上(如图2),求正方形
上(如图2),求正方形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究机构为了了解各年龄层对高考改革方案的关注程度,随机选取了200名年龄在![]() 内的市民进行了调查,并将结果绘制成如图所示的频率分布直方图(分第一~五组区间分别为
内的市民进行了调查,并将结果绘制成如图所示的频率分布直方图(分第一~五组区间分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).

(1)求选取的市民年龄在![]() 内的人数;
内的人数;
(2)若从第3,4组用分层抽样的方法选取5名市民进行座谈,再从中选取2人在座谈会中作重点发言,求作重点发言的市民中至少有一人的年龄在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】南方智运汽车公司在我市推出了共享汽车“Warmcar”,有一款车型为“众泰云”新能源共享汽车,其中一种租用方式“分时计费”规则为:0.15元/分钟+0.8元/公里.已知小李家离上班地点为10公里,每天租用该款汽车上、下班各一次,由于堵车、及红绿灯等原因每次路上开车花费的时间![]() (分钟)是一个随机变量,现统计了100次路上开车花费时间,在各时间段内是频数分布情况如下表所示:
(分钟)是一个随机变量,现统计了100次路上开车花费时间,在各时间段内是频数分布情况如下表所示:
时间 |
|
|
|
|
|
|
|
频数 | 2 | 6 | 14 | 36 | 28 | 10 | 4 |
(1)写出小李上班一次租车费用![]() (元)与用车时间
(元)与用车时间![]() (分钟)的函数关系;
(分钟)的函数关系;
(2)根据上面表格估计小李平均每次租车费用;
(3)“众泰云”新能源汽车还有一种租用方式为“按月计费”,规则为每个月收取租金2350元,若小李每个月上班时间平均按21天计算,在不计电费和情况下,请你为小李选择一种省钱的租车方式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,点
中,点![]() 是线段
是线段![]() 上的动点,则下列说法错误的是( )
上的动点,则下列说法错误的是( )
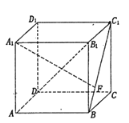
A. 当点![]() 移动至
移动至![]() 中点时,直线
中点时,直线![]() 与平面
与平面![]() 所成角最大且为
所成角最大且为![]()
B. 无论点![]() 在
在![]() 上怎么移动,都有
上怎么移动,都有![]()
C. 当点![]() 移动至
移动至![]() 中点时,才有
中点时,才有![]() 与
与![]() 相交于一点,记为点
相交于一点,记为点![]() ,且
,且![]()
D. 无论点![]() 在
在![]() 上怎么移动,异面直线
上怎么移动,异面直线![]() 与
与![]() 所成角都不可能是
所成角都不可能是![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com