
【题目】已知椭圆C的中心在原点,一个焦点F(-2,0),且长轴长与短轴长的比为![]() ,
,
(1)求椭圆C的方程;
(2)设点M(m,0)在椭圆C的长轴上,设点P是椭圆上的任意一点,若当![]() 最小时,点P恰好落在椭圆的右顶点,求实数m的取值范围.
最小时,点P恰好落在椭圆的右顶点,求实数m的取值范围.
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,侧面
中,侧面![]() ⊥底面
⊥底面![]() ,底面
,底面![]() 为直角梯形,
为直角梯形,![]() //
//![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.

(Ⅰ)求证:PA//平面BEF;
(Ⅱ)若PC与AB所成角为![]() ,求
,求![]() 的长;
的长;
(Ⅲ)在(Ⅱ)的条件下,求二面角F-BE-A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点.将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则三棱锥PDCE的外接球的体积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
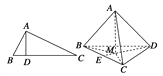
【题目】如图,在△ABC中,AB⊥AC,若AD⊥BC,则AB2=BD·BC;类似地有命题:在三棱锥A-BCD中,AD⊥平面ABC,若A点在平面BCD内的射影为M,则有S![]() =S△BCM·S△BCD.上述命题是 ( )
=S△BCM·S△BCD.上述命题是 ( )
A. 真命题
B. 增加条件“AB⊥AC”才是真命题
C. 增加条件“M为△BCD的垂心”才是真命题
D. 增加条件“三棱锥A-BCD是正三棱锥”才是真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,抛物线
,抛物线![]() 的准线被椭圆
的准线被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
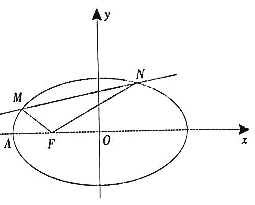
(2)如图,点![]() 分别是椭圆
分别是椭圆![]() 的左顶点、左焦点直线
的左顶点、左焦点直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() (
(![]() 都在
都在![]() 轴上方).且
轴上方).且![]() .证明:直线
.证明:直线![]() 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,若acos2![]() +ccos2
+ccos2![]() =
=![]() b.
b.
(1)求证:a,b,c成等差数列;
(2)若∠B=60°,b=4,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前我国城市的空气污染越来越严重,空气质量指数![]() 一直居高不下,对人体的呼吸系统造成了严重的影响,现调查了某城市500名居民的工作场所和呼吸系统健康,得到
一直居高不下,对人体的呼吸系统造成了严重的影响,现调查了某城市500名居民的工作场所和呼吸系统健康,得到![]() 列联表如下:
列联表如下:
室外工作 | 室内工作 | 合计 | |
有呼吸系统疾病 | 150 | ||
无呼吸系统疾病 | 100 | ||
合计 | 200 |
(Ⅰ)请把![]() 列联表补充完整;
列联表补充完整;
(Ⅱ)你是否有95%的把握认为感染呼吸系统疾病与工作场所有关;
(Ⅲ)现采用分层抽样从室内工作的居民中抽取一个容量为6的样本,将该样本看成一个总体,从中随机抽取2人,求2人都有呼吸系统疾病的概率.
参考公式与临界表:![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com