
【题目】某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为了研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,分别加以统计,得到如图所示的频率分布直方图.
,分别加以统计,得到如图所示的频率分布直方图.

(1)根据“25周岁以上组”的频率分布直方图,求25周岁以上组工人日平均生产件数的中位数的估计值(四舍五入保留整数);
(2)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至多抽到一名“25周岁以下组”工人的概率。
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】如图所示,圆锥的轴截面为等腰直角△SAB,Q为底面圆周上一点.

(1)若QB的中点为C,OH⊥SC,求证:OH⊥平面SBQ;
(2)如果∠AOQ=60°,QB=2![]() ,求此圆锥的体积.
,求此圆锥的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的部分图象如图所示,若将f(x)图象上的所有点向右平移
)的部分图象如图所示,若将f(x)图象上的所有点向右平移 ![]() 个单位得到函数g(x)的图象,则函数g(x)的单调递增区间为( )
个单位得到函数g(x)的图象,则函数g(x)的单调递增区间为( ) 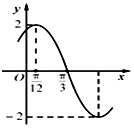
A.[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈Z
],k∈Z
B.[2kπ﹣ ![]() ,2kπ+
,2kπ+ ![]() ],k∈Z
],k∈Z
C.[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈Z
],k∈Z
D.[2kπ﹣ ![]() ,2kπ+
,2kπ+ ![]() ],k∈Z
],k∈Z
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的两个焦点分别为F1(﹣ ![]() ,0),F2(
,0),F2( ![]() ,0),且椭圆C过点P(3,2).
,0),且椭圆C过点P(3,2).
(1)求椭圆C的标准方程;
(2)与直线OP平行的直线交椭圆C于A,B两点,求△PAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2ωx+2 ![]() sinωxcosωx﹣cos2ωx(ω>0),f(x)的图象相邻两条对称轴的距离为
sinωxcosωx﹣cos2ωx(ω>0),f(x)的图象相邻两条对称轴的距离为 ![]() .
.
(1)求f( ![]() )的值;
)的值;
(2)将f(x)的图象上所有点向左平移m(m>0)个长度单位,得到y=g(x)的图象,若y=g(x)图象的一个对称中心为( ![]() ,0),当m取得最小值时,求g(x)的单调递增区间.
,0),当m取得最小值时,求g(x)的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】方程![]() 的曲线即为函数
的曲线即为函数![]() 的图像,对于函数
的图像,对于函数![]() ,有如下结论:①
,有如下结论:①![]() 在
在![]() 上单调递减;②函数
上单调递减;②函数![]() 不存在零点;③函数
不存在零点;③函数![]() 的值域是
的值域是![]() ;④
;④![]() 的图像不经过第一象限,其中正确结论的个数是___________
的图像不经过第一象限,其中正确结论的个数是___________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌汽车4S店,对该品牌旗下的A型、B型、C型汽车进行维修保养,每辆车一年内需要维修的人工费用为200元,汽车4S店记录了该品牌三种类型汽车各100辆到店维修的情况,整理得下表:
车型 | A型 | B型 | C型 |
频数 | 20 | 40 | 40 |
假设该店采用分层抽样的方法从上维修的100辆该品牌三种类型汽车中随机抽取10辆进行问卷回访.
(1)从参加问卷到访的10辆汽车中随机抽取两辆,求这两辆汽车来自同一类型的概率;
(2)某公司一次性购买该品牌A、B、C型汽车各一辆,记ξ表示这三辆车的一年维修人工费用总和,求ξ的分布列及数学期望(各型汽车维修的概率视为其需要维修的概率);
(3)经调查,该品牌A型汽车的价格与每月的销售量之间有如下关系:
价格(万元) | 25 | 23.5 | 22 | 20.5 |
销售量(辆) | 30 | 33 | 36 | 39 |
已知A型汽车的购买量y与价格x符合如下线性回归方程: ![]() =
= ![]() x+80,若A型汽车价格降到19万元,请你预测月销售量大约是多少?
x+80,若A型汽车价格降到19万元,请你预测月销售量大约是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com