
【题目】已知若椭圆![]() :
:![]() (
(![]() )交
)交![]() 轴于
轴于![]() ,
,![]() 两点,点
两点,点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() ,
,![]() 的任意一点,直线
的任意一点,直线![]() ,
,![]() 分别交
分别交![]() 轴于点
轴于点![]() ,
,![]() ,则
,则![]() 为定值
为定值![]() .
.
(1)若将双曲线与椭圆类比,试写出类比得到的命题;
(2)判定(1)类比得到命题的真假,请说明理由.
科目:高中数学 来源: 题型:
【题目】现计划用两张铁丝网在一片空地上围成一个梯形养鸡场![]() ,
,![]() ,
,![]() ,已知
,已知![]()
![]() 两段是由长为
两段是由长为![]() 的铁丝网折成,
的铁丝网折成,![]()
![]() 两段是由长为
两段是由长为![]() 的铁丝网折成.设上底
的铁丝网折成.设上底![]() 的长为
的长为![]() ,所围成的梯形面积为
,所围成的梯形面积为![]() .
.
(1)求S关于x的函数解析式,并求x的取值范围;
(2)当x为何值时,养鸡场的面积最大?最大面积为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着全民健康运动的普及,每天一万步已经成为一种健康时尚,某学校为了教职工健康工作,在全校范围内倡导“每天一万步”健步走活动,学校界定一人一天走路不足4千步为健步常人,不少于16千步为健步超人,其他为健步达人,学校随机抽查了36名教职工,其每天的走步情况统计如下:
步数 |
|
|
|
人数 | 6 | 18 | 12 |
现对抽查的36人采用分层抽样的方式选出6人
(1)求从这三类人中各抽多少人;
(2)现从选出的6人中随机抽取2人,求这两人健步类型相同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
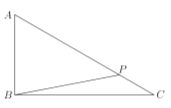
【题目】如图,某公园有三个警卫室![]() 、
、![]() 、
、![]() 有直道相连,
有直道相连,![]() 千米,
千米,![]() 千米,
千米,![]() 千米.
千米.
(1)保安甲沿![]() 从警卫室
从警卫室![]() 出发行至点
出发行至点![]() 处,此时
处,此时![]() ,求
,求![]() 的直线距离;
的直线距离;
(2)保安甲沿![]() 从警卫室
从警卫室![]() 出发前往警卫室
出发前往警卫室![]() ,同时保安乙沿
,同时保安乙沿![]() 从警卫室
从警卫室![]() 出发前往警卫室
出发前往警卫室![]() ,甲的速度为1千米/小时,乙的速度为2千米/小时,若甲乙两人通过对讲机联系,对讲机在公园内的最大通话距离不超过3千米,试问有多长时间两人不能通话?(精确到0.01小时)
,甲的速度为1千米/小时,乙的速度为2千米/小时,若甲乙两人通过对讲机联系,对讲机在公园内的最大通话距离不超过3千米,试问有多长时间两人不能通话?(精确到0.01小时)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某中学甲乙两班各6名学生,测量他们的身高(单位:cm),获得身高数据的茎叶图如下图.
甲班 2 9 1 0 8 2 | 18 17 16 | 乙班 0 0 1 4 7 3 |
(1)判断哪个班的平均身高较高, 并说明理由;
(2)计算甲班的样本方差;
(3)现从乙班这6名学生中随机抽取两名学生,求至少有一名身高不低于![]() 的学生被抽中的概率.
的学生被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,如果![]() 与
与![]() 都是整数,就称点
都是整数,就称点![]() 为整点,下列命题中正确的是_____________(写出所有正确命题的编号)
为整点,下列命题中正确的是_____________(写出所有正确命题的编号)
①存在这样的直线,既不与坐标轴平行又不经过任何整点
②如果![]() 与
与![]() 都是无理数,则直线
都是无理数,则直线![]() 不经过任何整点
不经过任何整点
③直线![]() 经过无穷多个整点,当且仅当
经过无穷多个整点,当且仅当![]() 经过两个不同的整点
经过两个不同的整点
④直线![]() 经过无穷多个整点的充分必要条件是:
经过无穷多个整点的充分必要条件是:![]() 与
与![]() 都是有理数
都是有理数
⑤存在恰经过一个整点的直线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com