
【题目】已知![]() .
.
(1)![]() 时,求
时,求![]() 的单调区间和最值;
的单调区间和最值;
(2)①若对于任意的![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围;②求证:
的取值范围;②求证:![]()
【答案】(1)减区间为![]() ,增区间为
,增区间为![]() ,最小值为
,最小值为![]() ,无最大值;(2)①
,无最大值;(2)①![]() ;②证明见解析.
;②证明见解析.
【解析】
(1)将![]() 代入函数
代入函数![]() 的解析式,求导,可知导函数在
的解析式,求导,可知导函数在![]() 上为增函数,观察可知导函数的唯一零点为
上为增函数,观察可知导函数的唯一零点为![]() ,进而得到函数
,进而得到函数![]() 的单调区间及最值;
的单调区间及最值;
(2)①先推导出![]() ,由
,由![]() 得出
得出![]() ,然后证明出
,然后证明出![]() 在
在![]() 恒成立即可,即可得出
恒成立即可,即可得出![]() ;
;
②利用①的结论及常见不等式![]() 容易得证.
容易得证.
(1)当![]() 时,
时,![]() ,则
,则![]() ,
,
易知![]() 单调递增,又
单调递增,又![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
所以,函数![]() 的减区间为
的减区间为![]() ,增区间为
,增区间为![]() ,
,
函数![]() 的最小值为
的最小值为![]() ,无最大值;
,无最大值;
(2)①必要性:若![]() ,则当
,则当![]() 时,
时,![]() ,不合乎题意,所以,必有
,不合乎题意,所以,必有![]() .
.
又![]() ,则
,则![]() ;
;
充分性:易知![]() .
.
故只要证明![]() 在
在![]() 恒成立即可,
恒成立即可,
即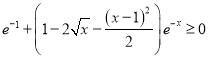 ,令
,令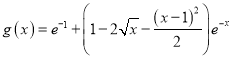 ,
,
则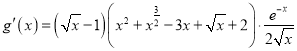
![]() ,
,
则![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,则
单调递增,则![]() .
.
故![]() ,因此,实数
,因此,实数![]() 的取值范围是
的取值范围是![]() ;
;
②由①可知,要证![]() ,只需证
,只需证![]() ,
,
先证明不等式![]() ,构造函数
,构造函数![]() ,
,![]() ,
,
![]() ,令
,令![]() ,可得
,可得![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以,函数![]() 的减区间为
的减区间为![]() ,增区间为
,增区间为![]() ,
,![]() ,
,
所以,对任意的![]() ,
,![]() .
.
![]() ,
,
故![]() 成立.
成立.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】设![]() 为实数,已知函数
为实数,已知函数![]() 的导函数为
的导函数为![]() ,且
,且![]() .
.
(1)求![]() 的值;
的值;
(2)设![]() 为实数,若对于任意
为实数,若对于任意![]() ,不等式
,不等式![]() 恒成立,且存在唯一的实数
恒成立,且存在唯一的实数![]() 使得
使得![]() 成立,求
成立,求![]() 的值;
的值;
(3)是否存在负数![]() ,使得
,使得![]() 是曲线
是曲线![]() 的切线.若存在,求出
的切线.若存在,求出![]() 的所有值:若不存在,请说明理由.
的所有值:若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校需从甲、乙两名学生中选一人参加物理竞赛,这两名学生最近5次的物理竞赛模拟成绩如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
学生甲的成绩(分) | 80 | 85 | 71 | 92 | 87 |
学生乙的成绩(分) | 90 | 76 | 75 | 92 | 82 |
(1)根据成绩的稳定性,现从甲、乙两名学生中选出一人参加物理竞赛,你认为选谁比较合适?
(2)若物理竞赛分为初赛和复赛,在初赛中有如下两种答题方案:方案1:每人从5道备选题中任意抽出1道,若答对,则可参加复赛,否则被淘汰;方案2:每人从5道备选题中任意抽出3道,若至少答对其中2道,则可参加复赛,否则被淘汰.若学生乙只会5道备选题中的3道,则学生乙选择哪种答题方案进入复赛的可能性更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个不透明的盒子中关有蝴蝶、蜜蜂和蜻蜓三种昆虫共11只,现在盒子上开一小孔,每次只能飞出1只昆虫(假设任意1只昆虫等可能地飞出).若有2只昆虫先后任意飞出(不考虑顺序),则飞出的是蝴蝶或蜻蜓的概率是![]() .
.
(1)求盒子中蜜蜂有几只;
(2)若从盒子中先后任意飞出3只昆虫(不考虑顺序),记飞出蜜蜂的只数为X,求随机变量X的分布列与数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+1,g(x)=4x+1,的定义域都是集合A,函数f(x)和g(x)的值域分别为S和T,
(1)若A=[1,2],求S∩T
(2)若A=[0,m]且S=T,求实数m的值
(3)若对于集合A的任意一个数x的值都有f(x)=g(x),求集合A.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一颗骰子投掷两次,第一次出现的点数记为a,第二次出现的点数记为b,设两条直线l1:ax+by=2与l2:x+2y=2平行的概率为P1,相交的概率为P2,则点P(36P1,36P2)与圆C:x2+y2=1 098的位置关系是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
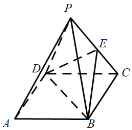
【题目】如图所示,底面为平行四边形ABCD的四棱锥P-ABCD中,E为PC的中点.求证:PA∥平面BDE.(要求注明每一步推理的大前提、小前提和结论,并最终把推理过程用简略的形式表示出来)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,双曲线![]() 的两顶点为
的两顶点为![]() ,
,![]() ,虚轴两端点为
,虚轴两端点为![]() ,
,![]() ,两焦点为
,两焦点为![]() ,
,![]() ,若以
,若以![]() 为直径的圆内切于菱形
为直径的圆内切于菱形![]() ,切点分别为
,切点分别为![]() ,
,![]() ,
,![]() ,
,![]() .则
.则
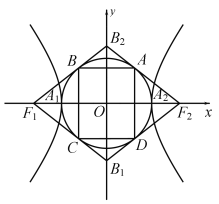
(1)双曲线的离心率![]() ______;
______;
(2)菱形![]() 的面积
的面积![]() 与矩形
与矩形![]() 的面积
的面积![]() 的比值
的比值![]() ______.
______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com