
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(1)函数![]() 的图象能否与
的图象能否与![]() 轴相切?若能与
轴相切?若能与![]() 轴相切,求实数
轴相切,求实数![]() 的值;否则,请说明理由;
的值;否则,请说明理由;
(2)若函数![]() 在
在![]() 上单调递增,求实数
上单调递增,求实数![]() 能取到的最大整数值.
能取到的最大整数值.
【答案】(1)见解析;(2)1.
【解析】【试题分析】(1)依据题设条件运用导数的几何意义建立方程进行分析求解;(2)依据题设条件借助等比数列的求和公式及等差数列的求和公式进行求解:
(1)![]() ,
,
假设函数![]() 的图象与
的图象与![]() 轴相切于点
轴相切于点![]() ,则有
,则有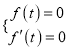 ,
,
即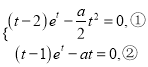 ,
,
由②可知![]() ,代入①中可得
,代入①中可得![]() .
.
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
∵![]() ,
,
∴方程![]() 无解,
无解,
故无论![]() 取何值,函数
取何值,函数![]() 的图象都不与
的图象都不与![]() 轴相切.
轴相切.
(2)记![]() ,
,
由题意知![]() 在
在![]() 上恒成立.
上恒成立.
由![]() ,可得,
,可得, ![]() 的必要条件是
的必要条件是![]() ,
,
若![]() ,则
,则![]() ,
,
当![]() 时,
时, ![]() ,故
,故![]() ,
,
下面证明:当![]() 时,不等式
时,不等式![]() 恒成立.
恒成立.
令![]() ,则
,则![]() .
.
记![]() ,则
,则![]() ,
,
当![]() 时,
时, ![]() 单调递增且
单调递增且![]() ;
;
当![]() 时,
时, ![]() 单调递减且
单调递减且![]() ,
,
∵![]() .
.
∴存在唯一的![]() 使得
使得![]() ,且当
,且当![]() 时,
时, ![]() ,
, ![]() 单调递减;
单调递减;
当![]() 时,
时, ![]() 单调递增.
单调递增.
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴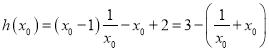 ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
从而![]() 恒成立,故
恒成立,故![]() 能取得的最大整数为1.
能取得的最大整数为1.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】在平面内有n(n∈N*)条直线,其中任何两条不平行,任何三条不过同一点,若这n条直线把平面分成f(n)个平面区域,则f(3)=;f(n)= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(文)已知矩形ABB1A1是圆柱体的轴截面,O、O1分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为2:1,且该圆柱体的体积为32π,如图所示. 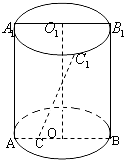
(1)求圆柱体的侧面积S侧的值;
(2)若C1是半圆弧 ![]() 的中点,点C在半径OA上,且OC=
的中点,点C在半径OA上,且OC= ![]() OA,异面直线CC1与BB1所成的角为θ,求sinθ的值.
OA,异面直线CC1与BB1所成的角为θ,求sinθ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:已知四棱锥P﹣ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,求证: 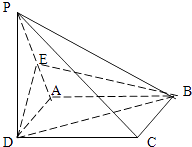
(1)PC∥平面EBD.
(2)平面PBC⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=x3+2x2﹣4x+5在[﹣4,1]上的最大值和最小值分别是( )
A.13, ![]()
B.4,﹣11
C.13,﹣11
D.13,最小值不确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com