
(本题满分13分)本题共有2个小题,第1小题满分6分,第2小题满分7分.
已知椭圆![]() :
:![]() (
(![]() )过点
)过点![]() ,其左、右焦点分别为
,其左、右焦点分别为![]() ,且
,且
![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 是直线
是直线![]() 上的两个动点,且
上的两个动点,且![]() ,则以
,则以![]() 为直径的圆
为直径的圆![]() 是否过定点?请说明理由.
是否过定点?请说明理由.
科目:高中数学 来源: 题型:
(本大题满分13分)本题共有2个小题,第1小题满分5分,第2小题满分8分.
如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝,骨架把圆柱底面8等份,再用S平方米塑料片制成圆柱的侧面和下底面(不安装上底面).
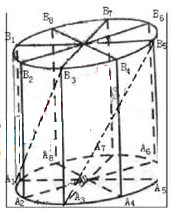 (1)当圆柱底面半径
(1)当圆柱底面半径![]() 取何值时,
取何值时,![]() 取得最大值?并求出该
取得最大值?并求出该
最大值(结果精确到0.01平方米);
(2)在灯笼内,以矩形骨架的顶点为点,安装一些霓虹灯,当灯笼的底面半径为0.3米时,求图中两根直线![]() 与
与![]() 所在异面直线所成角的大小(结果用反三角函数表示)
所在异面直线所成角的大小(结果用反三角函数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
(本大题满分13分)本题共有2个小题,第1小题满分5分,第2小题满分8分.
如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝,骨架把圆柱底面8等份,再用S平方米塑料片制成圆柱的侧面和下底面(不安装上底面).
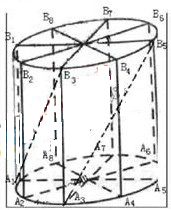 (1)当圆柱底面半径
(1)当圆柱底面半径![]() 取何值时,
取何值时,![]() 取得最大值?并求出该
取得最大值?并求出该
最大值(结果精确到0.01平方米);
(2)在灯笼内,以矩形骨架的顶点为点,安装一些霓虹灯,当灯笼的底面半径为0.3米时,求图中两根直线![]() 与
与![]() 所在异面直线所成角的大小(结果用反三角函数表示)
所在异面直线所成角的大小(结果用反三角函数表示)
查看答案和解析>>
科目:高中数学 来源:2011届福建厦门双十中学高三考前热身理数试卷 题型:解答题
(本小题满分13分)
已知数列 满足
满足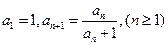 ,数列
,数列 满足
满足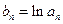 ,数列
,数列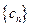
满足 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ) ,
,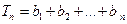 ,试比较
,试比较 与
与 的大小,并证明;
的大小,并证明;
(Ⅲ)我们知道数列 如果是等差数列,则公差
如果是等差数列,则公差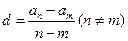 是一个常数,显然在本题的数列
是一个常数,显然在本题的数列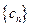 中,
中, 不是一个常数,但
不是一个常数,但 是否会小于等于一个常数
是否会小于等于一个常数 呢,若会,请求出
呢,若会,请求出 的范围,若不会,请说明理由.
的范围,若不会,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建厦门双十中学高三考前热身理数试卷 题型:解答题
(本小题满分13分)
已知数列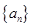 满足
满足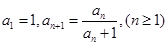 ,数列
,数列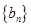 满足
满足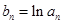 ,数列
,数列
满足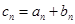 .
.
(Ⅰ)求数列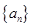 的通项公式;
的通项公式;
(Ⅱ) ,
,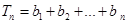 ,试比较
,试比较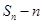 与
与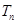 的大小,并证明;
的大小,并证明;
(Ⅲ)我们知道数列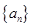 如果是等差数列,则公差
如果是等差数列,则公差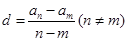 是一个常数,显然在本题的数列
是一个常数,显然在本题的数列 中,
中, 不是一个常数,但
不是一个常数,但 是否会小于等于一个常数
是否会小于等于一个常数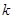 呢,若会,请求出
呢,若会,请求出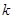 的范围,若不会,请说明理由.
的范围,若不会,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分13分)
已知数列![]() 满足
满足![]() ,数列
,数列![]() 满足
满足![]() ,数列
,数列![]()
满足![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)![]() ,
,![]() ,试比较
,试比较![]() 与
与![]() 的大小,并证明;
的大小,并证明;
(Ⅲ)我们知道数列![]() 如果是等差数列,则公差
如果是等差数列,则公差![]() 是一个常数,显然在本题的数列
是一个常数,显然在本题的数列![]() 中,
中,![]() 不是一个常数,但
不是一个常数,但![]() 是否会小于等于一个常数
是否会小于等于一个常数![]() 呢,若会,请求出
呢,若会,请求出![]() 的范围,若不会,请说明理由.
的范围,若不会,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com