
【题目】将一个半径适当的小球放入如图所示的容器自上方的入口处,小球自由下落,小气在下落的过程中,将遇到黑色障碍物3次,最后落入A袋或B袋中,已知小球每次遇到障碍物时,向左、右两边下落的概率分别是 ![]() ,
, ![]()
(1)分别求出小球落入A袋和B袋中的概率;
(2)在容器 入口处依次放入4个小球,记ξ为落入B袋中的小球个数,求ξ的分布列和数学期望.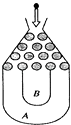
【答案】
(1)
解:记“小球落入A袋中”为事件M”,小球落入B袋中”为事件N,则事件M的对立事件N,
而小球落入A袋中当且仅当小球一直向左落下或一直向右落下,
故P(M)= ![]() +
+ ![]() =
= ![]() ,
,
从而P(N)=1﹣P(M)=1﹣ ![]() =
= ![]() .
.
(2)
解:显然,随机变量ξ的所有可能的取值为0,1,2,3,4
且B(4, ![]() ),
),
故P(ξ=0)= ![]() ×(
×( ![]() )0×(
)0×( ![]() )4=
)4= ![]() ,
,
P(ξ=1)= ![]() ×(
×( ![]() )1×(
)1×( ![]() )3=
)3= ![]() ,
,
P(ξ=2)= ![]() ×(
×( ![]() )2×(
)2×( ![]() )2=
)2= ![]() ,
,
P(ξ=3)= ![]() ×(
×( ![]() )3×(
)3×( ![]() )1=
)1= ![]() ,
,
P(ξ=4)= ![]() ×(
×( ![]() )4×(
)4×( ![]() )0=
)0= ![]() ,
,
则ξ的分布列为:
ξ | 0 | 1 | 2 | 3 | 4 |
P |
|
|
|
|
|
故ξ的数学期望为E(ξ)=4× ![]() =
= ![]()
【解析】(1)设出“小球落入A袋中”为事件M”,小球落入B袋中”为事件N,则事件M的对立事件N,而小球落入A袋中当且仅当小球一直向左落下或一直向右落下,运用对立事件求解即可.(2)确定随机变量ξ的所有可能的取值为0,1,2,3,4判断出二项分布,得出B(4, ![]() ),运用概率公式求解即可.
),运用概率公式求解即可.
【考点精析】掌握离散型随机变量及其分布列是解答本题的根本,需要知道在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知a为实数,f(x)=(x2﹣4)(x﹣a).
(1)求导数f′(x);
(2)若f′(﹣1)=0,求f(x)在[﹣2,2]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合M={1,2,3},N={1,2,3,4},定义函数f:M→N.若点A(1,f(1))、B(2,f(2))、C(3,f(3)),△ABC的外接圆圆心为D,且 ![]() ,则满足条件的函数f(x)有( )
,则满足条件的函数f(x)有( )
A.6个
B.10个
C.12个
D.16个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着人们对环境关注度的提高,绿色低碳出行越来越受到市民重视. 为此贵阳市建立了公共自行车服务系统,市民凭本人二代身份证到自行车服务中心办理诚信借车卡借车,初次办卡时卡内预先赠送20积分,当积分为0时,借车卡将自动锁定,限制借车,用户应持卡到公共自行车服务中心以1元购1个积分的形式再次激活该卡,为了鼓励市民租用公共自行车出行,同时督促市民尽快还车,方便更多的市民使用,公共自行车按每车每次的租用时间进行扣分收费,具体扣分标准如下:
①租用时间不超过1小时,免费;
②租用时间为1小时以上且不超过2小时,扣1分;
③租用时间为2小时以上且不超过3小时,扣2分;
④租用时间超过3小时,按每小时扣2分收费(不足1小时的部分按1小时计算).
甲、乙两人独立出行,各租用公共自行车一次,两人租车时间都不会超过3小时,设甲、乙租用时间不超过1小时的概率分别是0.4和0.5;租用时间为1小时以上且不超过2小时的概率分别是0.4和0.3.
(1)求甲、乙两人所扣积分相同的概率;
(2)设甲、乙两人所扣积分之和为随机变量![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,M是正方体ABCD﹣A1B1C1D1的棱DD1的中点,给出下列命题
①过M点有且只有一条直线与直线AB、B1C1都相交;
②过M点有且只有一条直线与直线AB、B1C1都垂直;
③过M点有且只有一个平面与直线AB、B1C1都相交;
④过M点有且只有一个平面与直线AB、B1C1都平行.
其中真命题是( )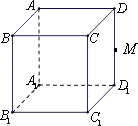
A.②③④
B.①③④
C.①②④
D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,矩形ABCD的边AB=m,BC=4,PA⊥平面ABCD,PA=3,现有数据:
① ![]() ;②m=3;③m=4;④
;②m=3;③m=4;④ ![]() .若在BC边上存在点Q(Q不在端点B、C处),使PQ⊥QD,则m可以取( )
.若在BC边上存在点Q(Q不在端点B、C处),使PQ⊥QD,则m可以取( )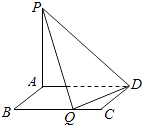
A.①②
B.①②③
C.②④
D.①
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com