
 的图象上的点 Pn(tn2,tn)(n=1,2,…)与x轴正半轴上的点Qn及原点O构成一系列正△PnQn-1Qn(Q与O重合),记an=|QnQn-1|
的图象上的点 Pn(tn2,tn)(n=1,2,…)与x轴正半轴上的点Qn及原点O构成一系列正△PnQn-1Qn(Q与O重合),记an=|QnQn-1| =
=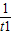 =tan
=tan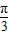 =
= ,由此能求出a1的值.
,由此能求出a1的值.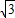 (x-tn2),故Qn-1(tn2-
(x-tn2),故Qn-1(tn2- ,0),由直线 PnQn的方程为:y-tn=-
,0),由直线 PnQn的方程为:y-tn=- (x-tn2),得 Qn(tn2+
(x-tn2),得 Qn(tn2+ ,0),故tn2-
,0),故tn2- =tn-12+
=tn-12+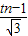 ,由此能求出an.
,由此能求出an. ,由此能求出k 的最小值.
,由此能求出k 的最小值.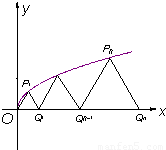 解:(1)∵P1(t12,t1)(t>0),…(1分),
解:(1)∵P1(t12,t1)(t>0),…(1分),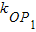 =
=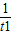 =tan
=tan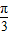 =
= ,解得t1=
,解得t1= ,
, ,
,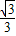 ),a1=|Q1Q|=|OP1|=
),a1=|Q1Q|=|OP1|= .…(5分)
.…(5分) (x-tn2),
(x-tn2), ,0),
,0),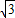 (x-tn2),
(x-tn2), ,0)
,0)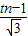 ,0),故tn2-
,0),故tn2- =tn-12+
=tn-12+ ,
,
 (n-1)=
(n-1)= n.…(8分)
n.…(8分) n(n+1),0),Qn-1(
n(n+1),0),Qn-1( n(n-1),0),
n(n-1),0), n.…(10分)
n.…(10分) ,…(14分)
,…(14分)

 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:填空题
 ,则该函数为偶函数;
,则该函数为偶函数;查看答案和解析>>
科目:高中数学 来源:2009-2010学年高一(上)11月调研数学试卷(必修1)(解析版) 题型:填空题
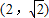 ,则该函数为偶函数;
,则该函数为偶函数;查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省淮安市淮阴中学高三(上)期末数学复习试卷(四)(解析版) 题型:解答题
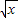 的图象上的点 Pn(tn2,tn)(n=1,2,…)与x轴正半轴上的点Qn及原点O构成一系列正△PnQn-1Qn(Q与O重合),记an=|QnQn-1|
的图象上的点 Pn(tn2,tn)(n=1,2,…)与x轴正半轴上的点Qn及原点O构成一系列正△PnQn-1Qn(Q与O重合),记an=|QnQn-1|查看答案和解析>>
科目:高中数学 来源:新课标高三数学对数与对数函数、反比例函数与幂函数专项训练(河北) 题型:单选题
下列命题:
①幂函数的图象都经过点(1,1)和点(0,0);②幂函数的图象不可能在第四象限;③当n=0时,函数y=xn的图象是一条直线;④幂函数y=xn,当n>0时是增函数;⑤幂函数y=xn,当n<0时,在第一象限内函数值随x值的增大而减小.
其中正确命题的序号是:________(把你认为正确的命题的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com