在三角形△ABC中,a,b,c分别为角A、B、C所对的边,sin2C=sin(A+B)•sin(A-B)则A= ;若a=6,则三角形ABC内切圆半径r的最大值是 .
【答案】
分析:结合三角形的内角和公式可得A+B=π-C,代入已知sin
2C=sin(A+B)•sin(A-B)化简可得,sinC=sin(A-B),根据角的范围从而可得A-B=C或A-B+C=π,从而可求结果;根据当三角形是一个等腰直角三角形时,内切圆的半径最大,根据勾股定理得到结果.
解答:解:∵A+B=π-C,
∴sin
2C=sin(π-C)•sin(A-B)
∴sin
2C=sinC•sin(A-B)
∴sinC=sin(A-B)
∴C=A-B或C+A-B=π(舍去)
∴C+B=A
∴A=
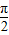
∵当三角形是一个等腰直角三角形时,内切圆的半径最大,
∴直角边的长度是x,有2x
2=36
∴x=3
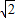
根据从圆外一点引圆的两条切线,切线长度相等,
得到内切圆的半径是3
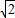
-3
故答案为:
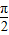
;
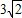
-3
点评:本题主要考查了三角形的内角和公式和诱导公式,本题解题的关键是根据三角形内角和做出结果,本题是一个基础题.

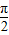
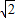
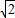 -3
-3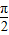 ;
;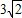 -3
-3

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案