
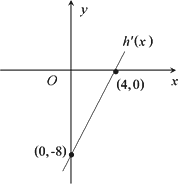
已知二次函数h(x)=ax2+bx+c(其中c<3),其导函数 的图象如图,f(x)=6lnx+h(x).
的图象如图,f(x)=6lnx+h(x).

①求f(x)在x=3处的切线斜率;
②若f(x)在区间(m,m+ )上是单调函数,求实数m的取值范围;
)上是单调函数,求实数m的取值范围;
③若对任意k∈[-1,1],函数y=kx(x∈(0,6])的图象总在函数y=f(x)图象的上方,求c的取值范围.
①0; ②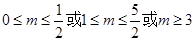 ;③
;③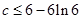
【解析】
试题分析:①根据图像求出一次导函数的解析式,那么函数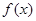 的导函数就很容易得到了,所求的切线斜率即是其所对应的的导函数值;②根据函数的单调性与导数的关系求出函数的三个单调区间,使得所给的区间在任何一个单调区间内即可求出未知数的取值范围;③由已知条件先导出和
的导函数就很容易得到了,所求的切线斜率即是其所对应的的导函数值;②根据函数的单调性与导数的关系求出函数的三个单调区间,使得所给的区间在任何一个单调区间内即可求出未知数的取值范围;③由已知条件先导出和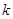 有关的不等式,将
有关的不等式,将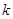 放在不等式的一边,那么就有
放在不等式的一边,那么就有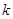 的最小值也要大于等于不等式另一边式子的最大值,才能保证不等式恒成立,由函数的单调性和导数的关系求最值即可.
的最小值也要大于等于不等式另一边式子的最大值,才能保证不等式恒成立,由函数的单调性和导数的关系求最值即可.
试题解析:①由已知得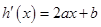 ,其图像如图所示过点
,其图像如图所示过点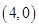 和
和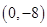 ,
,
则有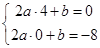 ,解得
,解得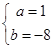 ,所以
,所以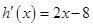 ,
,
所以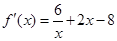 ,则
,则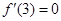 即
即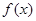 在
在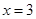 处的切线斜率为0;
3分
处的切线斜率为0;
3分
②由已知得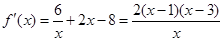
 ,
,
令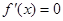 ,得
,得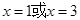 ,列表如下:
,列表如下:
|
x |
(0,1) |
1 |
(1, 3) |
3 |
(3,+∞) |
|
|
+ |
0 |
- |
0 |
+ |
|
..f(x) |
|
极大值 |
|
极小值 |
|
要使f(x)在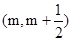 上是单调函数,则区间
上是单调函数,则区间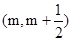 必须完全含在任意一个单调区间内, 5分
必须完全含在任意一个单调区间内, 5分
所以有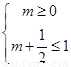 或
或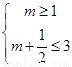 或
或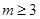 ,
,
所以m的取值范围为: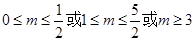 ;
7分
;
7分
③由题意知: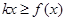 对
对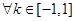 ,
,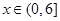 恒成立,
恒成立,
即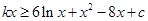 在
在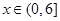 恒成立,
恒成立,
即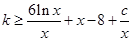 在
在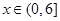 恒成立,
8分
恒成立,
8分
令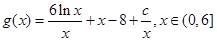 ,则
,则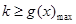 ,
,
因为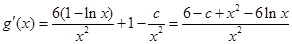 ,
,
令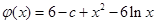 ,
, 则
则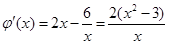 ,
,
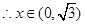 时,
时,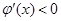 ,则
,则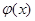 在
在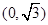 上是单调递减的,
上是单调递减的,
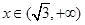 时,
时,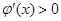 ,则
,则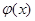 在
在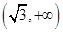 上是单调递增的,
上是单调递增的,
∴当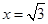 时,
时,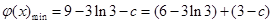 ,
,
又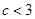 ,
,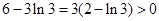 ,则
,则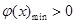 ,
,
所以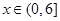 ,
,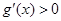 恒成立,则
恒成立,则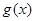 在
在 上是单调递增的,
上是单调递增的,
则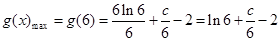 ,
.12分
,
.12分
 在
在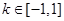 恒成立,
恒成立,
∴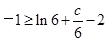 ,∴
,∴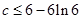 .
14分
.
14分
考点:函数的单调性和导数的关系,恒成立问题的解法.


科目:高中数学 来源:必修一教案数学苏教版 苏教版 题型:044
求函数解析式:
(1)已知一次函数f(x)满足f(0)=5,图象过点(-2,1),求f(x);
(2)已知二次函数g(x)满足g(1)=1,g(-1)=5,图象过原点,求g(x);
(3)已知二次函数h(x)与x轴的两交点为(-2,0),(3,0),且h(0)=-3,求h(x);
(4)已知二次函数F(x),其图象的顶点是(-1,2),且经过原点,求F(x).
查看答案和解析>>
科目:高中数学 来源:河北省三河一中2012届高三第二次月考数学理科试题 题型:044
已知二次函数h(x)=ax2+bx+c(其中c<3),其导函数y=![]() (x)的图象如图,f(x)=6lnx+h(x).
(x)的图象如图,f(x)=6lnx+h(x).
(1)求函数f(x)在x=3处的切线斜率;
(2)若函数y=-x,x∈(0,6]的图像总在函数y=f(x)图象的上方,求c的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川达州普通高中高三第一次诊断检测理科数学试卷(解析版) 题型:解答题
已知二次函数h(x)=ax2+bx+c(其中c<3),其导函数 的图象如图,f(x)=6lnx+h(x)
的图象如图,f(x)=6lnx+h(x)

(1)求f(x)在x=3处的切线斜率;
(2)若f(x)在区间(m,m+ )上是单调函数,求实数m的取值范围;
)上是单调函数,求实数m的取值范围;
(3)若对任意k∈[-1,1],函数y=kx(x∈(0,6])的图象总在函数y=f(x)图象的上方,求c的取值范围
查看答案和解析>>
科目:高中数学 来源:2013届浙江省高二下学期第一次统练理科数学试卷(解析版) 题型:解答题
已知二次函数h(x)=ax2+bx+c(c>0),其导函数y=h′(x)的图象如下,且f(x)=ln x-h(x).
(1)求函数f(x)在x=1处的切线斜率;
(2)若函数f(x)在上是单调函数,求实数m的取值范围;
(3)若函数y=2x-lnx(x∈[1,4])的图象总在函数y=f(x)的图象的上方,求c的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com