
【题目】下列四个命题中,其中错误的个数是()
①经过球面上任意两点,可以作且只可以作一个大圆;
②经过球直径的三等分点,作垂直于该直径的两个平面,则这两个平面把球面分成三部分的面积相等;
③球的面积是它大圆面积的四倍;
④球面上两点的球面距离,是这两点所在截面圆上,以这两点为端点的劣弧的长.
A. 0B. 1C. 2D. 3
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]()
(1)若a=1,b=2,求函数在点(2,f(2))处的切线方程;
(2)求函数的单调区间;
(3)若a<b,任取![]() 存在实数m使
存在实数m使![]() 恒成立,求m的取值范围.
恒成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,经过椭圆
,经过椭圆![]() 的右焦点的弦中最短弦长为2.
的右焦点的弦中最短弦长为2.
(1)求椭圆的![]() 的方程;
的方程;
(2)已知椭圆![]() 的左顶点为
的左顶点为![]() 为坐标原点,以
为坐标原点,以![]() 为直径的圆上是否存在一条切线
为直径的圆上是否存在一条切线![]() 交椭圆
交椭圆![]() 于不同的两点
于不同的两点![]() ,且直线
,且直线![]() 与
与![]() 的斜率的乘积为
的斜率的乘积为![]() ?若存在,求切线
?若存在,求切线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年开始,国家逐步推行全新的高考制度.新高考不再分文理科,采用3+3模式,其中语文、数学、外语三科为必考科目,满分各150分,另外考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物6门科目中自选3门参加考试(6选3),每科目满分100分.为了应对新高考,某高中从高一年级1000名学生(其中男生550人,女生450人)中,根据性别分层,采用分层抽样的方法从中抽取100名学生进行调查.
(1)学校计划在高一上学期开设选修中的“物理”和“地理”两个科目,为了了解学生对这两个科目的选课情况,对抽取到的100名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目),如表是根据调查结果得到的2×2列联表.请将列联表补充完整,并判断是否有99%的把握认为选择科目与性别有关?说明你的理由;
(2)在抽取到的女生中按(1)中的选课情况进行分层抽样,从中抽出9名女生,再从这9名女生中随机抽取4人,设这4人中选择“地理”的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
选择“物理” | 选择“地理” | 总计 | |
男生 | 10 | ||
女生 | 25 | ||
总计 |
附参考公式及数据:![]() ,其中
,其中![]() .
.
| 0.05 | 0.01 |
| 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,棱长为![]() 的正方形
的正方形![]() 中,点
中,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点,且
上的点,且![]() ,将
,将![]() ,
,![]() 沿
沿![]() ,
,![]() 折起,使得
折起,使得![]() ,
,![]() 两点重合于
两点重合于![]() 点上,设
点上,设![]() 与
与![]() 交于
交于![]() 点,过点
点,过点![]() 作
作![]() 于
于![]() 点.
点.
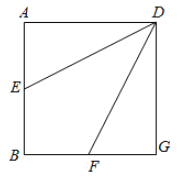
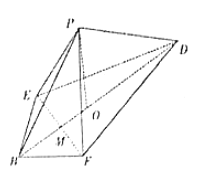
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是矩形,面
是矩形,面![]() 底面
底面![]() ,且
,且![]() 是边长为
是边长为![]() 的等边三角形,
的等边三角形, ![]() 在
在![]() 上,且
上,且![]() 面
面![]() .
.

(1)求证: ![]() 是
是![]() 的中点;
的中点;
(2)在![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 为直角?若存在,求出
为直角?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的左、右焦点分别为F1,F2,离心率为
的左、右焦点分别为F1,F2,离心率为![]() ,P为椭圆C上的动点,且满足
,P为椭圆C上的动点,且满足![]() ,
,![]() ,
,![]() 面积的最大值为4.
面积的最大值为4.
(1)求动点Q的轨迹E的方程和椭圆C的方程.
(2)若点P不在x轴上,过点F2作OP的平行线交曲线C于M、N两个不同的点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一个四位数的各位数字相加和为![]() ,则称该数为“完美四位数”,如数字“
,则称该数为“完美四位数”,如数字“![]() ”.试问用数字
”.试问用数字![]() 组成的无重复数字且大于
组成的无重复数字且大于![]() 的“完美四位数”有( )个
的“完美四位数”有( )个
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某学校高三年级800名学生中随机抽取50名测量身高,据测量被抽取的学生的身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160);第二组[160,165);…第八组[190,195],图是按上述分组方法得到的条形图.

(1)根据已知条件填写将表格填写完整;
组别 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
样本 | 2 | 4 | 10 | 10 | 15 | 4 |
(2)估计这所学校高三年级800名学生中身高在180cm以上(含180cm)的人数;
(3)在样本中,若第二组有1人为男生,其余为女生,第七组有1人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为一男一女的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com