
 =
= . …(4分)
. …(4分) =
= .…(4分)
.…(4分) =
= .…(6分)
.…(6分)

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:
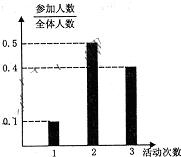 (理科)某中学号召学生在2010年春节期间至少参加一次社会公益活动(下面简称为“活动”).该校合唱团共有100名学生,他们参加活动的次数统计如图所示.
(理科)某中学号召学生在2010年春节期间至少参加一次社会公益活动(下面简称为“活动”).该校合唱团共有100名学生,他们参加活动的次数统计如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2013届广东省高二上学期期中考试文科数学 题型:解答题
(本小题满分14分)先后抛掷一枚骰子两次,将得到的点数分别记为 ,
, 。
。
(1)求 的概率;
的概率;
(2)求点 在函数
在函数 图像上的概率;
图像上的概率;
(3)将 的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率。
的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com