
分析 由一元二次方程根与系数的关系可得tanAtanC=1,则有A+C=$\frac{π}{2}$.由此可知△ABC为以角B为直角的直角三角形,由勾股定理结合不等式的性质求得ac的最大值,则△ABC面积的最大值可求.
解答 解:∵tanA,tanC是关于x的方程x2-(p-1)x+1=0的两个实根,
∴tanAtanC=1,则A+C=$\frac{π}{2}$.
∴B=$\frac{π}{2}$.
又b=2,
∴4=b2=a2+c2≥2ac,
当且仅当a=c时取等号.
∴${S}_{△ABC}=\frac{1}{2}ac≤1$.
故答案为:1.
点评 本题考查一元二次方程根与系数的关系,考查了同角三角函数基本关系式的应用,考查三角形面积的求法,是中档题.


科目:高中数学 来源: 题型:解答题
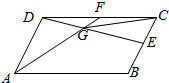 如图,已知E,F分别是平行四边形ABCD的边BC,CD中点,AF与DE相交于点G,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,则$\overrightarrow{GC}$=$\frac{3}{5}\overrightarrow{a}+\frac{1}{5}\overrightarrow{b}$(用$\overrightarrow{a}$,$\overrightarrow{b}$表示)
如图,已知E,F分别是平行四边形ABCD的边BC,CD中点,AF与DE相交于点G,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,则$\overrightarrow{GC}$=$\frac{3}{5}\overrightarrow{a}+\frac{1}{5}\overrightarrow{b}$(用$\overrightarrow{a}$,$\overrightarrow{b}$表示)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{4}$ | B. | -$\frac{7}{4}$ | C. | -$\frac{5}{4}$ | D. | -$\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{20}$ | B. | $\frac{13}{100}$ | C. | $\frac{3}{25}$ | D. | $\frac{7}{50}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-tanx | B. | y=cos(2x-$\frac{π}{2}$) | C. | y=sin2x+cos2x | D. | y=2cos2x-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{π}{6}$] | B. | (0,$\frac{π}{3}$] | C. | (0,$\frac{π}{2}$] | D. | [$\frac{π}{3}$,$\frac{2π}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-x-1 | B. | y=x+1 | C. | y=x-1 | D. | y=-x+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com