
【题目】已知椭圆![]() 的离心率
的离心率![]() ,
,![]() 是椭圆
是椭圆![]() 上一点.
上一点.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 的斜率为
的斜率为![]() ,且直线
,且直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,点
两点,点![]() 关于原点的对称点为
关于原点的对称点为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上一点,判断直线
上一点,判断直线![]() 与
与![]() 的斜率之和是否为定值,如果是,请求出此定值,如果不是,请说明理由.
的斜率之和是否为定值,如果是,请求出此定值,如果不是,请说明理由.
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)[选修4-4,极坐标与参数方程选讲]
在直角坐标系x0y中,曲线C1的参数方程为![]() (
(![]() 为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为p=4sin9
为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为p=4sin9
(1)求曲线C1的普通方程和C2的直角坐标方程;
(Ⅱ)已知曲线C3的极坐标方程为![]() =α,(0<α<x,p∈R),点A是曲线C3与C1的交点,点B是曲线C3与C2的交点,且A,B均异于原点O,且|AB|=4
=α,(0<α<x,p∈R),点A是曲线C3与C1的交点,点B是曲线C3与C2的交点,且A,B均异于原点O,且|AB|=4![]() ,求实数α的值
,求实数α的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代有着辉煌的数学研究成果,其中的《周髀算经》、《九章算术》、《海岛算经》、《孙子算经》、《缉古算经》,有丰富多彩的内容,是了解我国古代数学的重要文献,这5部专著中有3部产生于汉、魏、晋、南北朝时期,某中学拟从这5部专著中选择2部作为“数学文化”校本课程学习内容,则所选2部专著中至少有一部是汉、魏、晋、南北朝时期专著的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,∠BAC=120°,AC=AB=2,AA1=3.
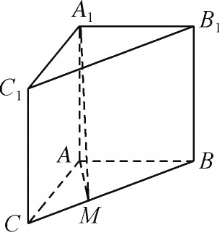
(1)求三棱柱ABC-A1B1C1的体积;
(2)若M是棱BC的一个靠近点C的三等分点,求二面角A-A1M-B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆A:(x+1)2+y2=16,圆C过点B(1,0)且与圆A相切,设圆心C的轨迹为曲线E.
(Ⅰ)求曲线E的方程;
(Ⅱ)过点B作两条互相垂直的直线l1,l2,直线l1与E交于M,N两点,直线l2与圆A交于P,Q两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点的序列![]() ,其中
,其中![]() .(
.(![]() 是线段
是线段![]() 的中点,
的中点,![]() 是线段
是线段![]() 的中点,……,
的中点,……,![]() 是线段
是线段![]() 的中点,…)
的中点,…)
(1)写出![]() 与
与![]() 之间的关系
之间的关系![]() ;
;
(2)设![]() ,计算
,计算![]() ,由此推测数列
,由此推测数列![]() 的通项公式,并且加以证明;
的通项公式,并且加以证明;
(3)求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知如图1直角梯形![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,沿
的中点,沿![]() 将梯形
将梯形![]() 折起(如图2),使平面
折起(如图2),使平面![]() 平面
平面![]() .
.
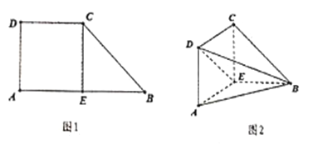
(1)证明![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人做下面的游戏:有一个由两个同轴圆柱组成的有盖容器,如图,里面的实心圆柱底面半径为![]() ,外面的圆柱面的底面半径为
,外面的圆柱面的底面半径为![]() ,容器的高为
,容器的高为![]() 。在容器内放入
。在容器内放入![]() 个半径为
个半径为![]() 且质地相同的小球,其中红、黄、蓝色各
且质地相同的小球,其中红、黄、蓝色各![]() 个,随意翻动容器,然后将容器直立在桌面上。当小球全部停止后,如果有两个颜色相同的小球相邻,则甲胜,否则乙胜。那么,甲胜的概率为()。
个,随意翻动容器,然后将容器直立在桌面上。当小球全部停止后,如果有两个颜色相同的小球相邻,则甲胜,否则乙胜。那么,甲胜的概率为()。

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com