
【题目】某盒子内装有三种颜色的玻璃球,一位同学每次从中随机拿出一个玻璃球,观察颜色后再放回,重复了50次,得到的信息如下:观察到红色26次、蓝色13次.如果从这个盒子内任意取一个玻璃球,估计:
(1)这个球既不是红色也不是蓝色的概率;
(2)这个球是红色或者是蓝色的概率.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左.右焦点为
的左.右焦点为![]() ,离心率为
,离心率为![]() .直线
.直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,
,![]() 是直线
是直线![]() 与椭圆
与椭圆![]() 的一个公共点,
的一个公共点,![]() 是点
是点![]() 关于直线
关于直线![]() 的对称点,设
的对称点,设![]() .
.
(1)证明:![]() ;
;
(2)若![]() ,
,![]() 的周长为
的周长为![]() ;写出椭圆
;写出椭圆![]() 的方程;
的方程;
(3)确定![]() 的值,使得
的值,使得![]() 是等腰三角形.
是等腰三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学生在开学季准备销售一种文具盒进行试创业,在一个开学季内,每售出1盒该产品获利润30元,未售出的产品,每盒亏损10元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了160盒该产品,以![]() (单位:盒,
(单位:盒, ![]() )表示这个开学季内的市场需求量,
)表示这个开学季内的市场需求量, ![]() (单位:元)表示这个开学季内经销该产品的利润.
(单位:元)表示这个开学季内经销该产品的利润.
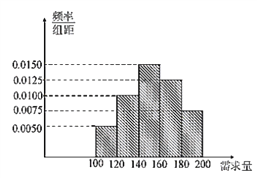
(1)根据直方图估计这个开学季内市场需求量![]() 的平均数;
的平均数;
(2)将![]() 表示为
表示为![]() 的函数;
的函数;
(3)根据直方图估计利润![]() 不少于4000元的概率.
不少于4000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有以下四种变换方式:
![]() 向左平移
向左平移![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的![]() 倍
倍![]() 纵坐标不变
纵坐标不变![]() ;
;
![]() 向左平移
向左平移![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的![]() 倍
倍![]() 纵坐标不变
纵坐标不变![]() ;
;
![]() 把各点的横坐标缩短到原来的
把各点的横坐标缩短到原来的![]() 倍
倍![]() 纵坐标不变
纵坐标不变![]() ,再向左平移
,再向左平移![]() 个单位长度;
个单位长度;
![]() 把各点的横坐标缩短到原来的
把各点的横坐标缩短到原来的![]() 倍
倍![]() 纵坐标不变
纵坐标不变![]() ,再向左平移
,再向左平移![]() 个单位长度;
个单位长度;
其中能将函数![]() 的图象变为函数
的图象变为函数![]() 的图象的是
的图象的是![]()
![]()
A. ![]() 和
和![]() B.
B. ![]() 和
和![]() C.
C. ![]() 和
和![]() D.
D. ![]() 和
和![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面几种推理是合情推理的是( )
①由圆的性质类比出球的有关性质;
②由直角三角形、等腰三角形、等边三角形内角和是![]() 归纳出所有三角形的内角和都是
归纳出所有三角形的内角和都是![]()
③由![]() ,满足
,满足![]() ,推出
,推出![]() 是奇函数;
是奇函数;
④三角形内角和是![]() ,四边形内角和是
,四边形内角和是![]() ,五边形内角和是
,五边形内角和是![]() ,由此得凸多边形内角和是
,由此得凸多边形内角和是![]() .
.
A. ①②④B. ①③④C. ②④D. ①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是( )
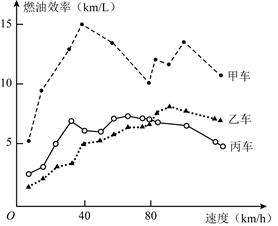
A. 消耗1升汽油,乙车最多可行驶5千米
B. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C. 甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D. 某城市机动车最高限速80千米/小时. 相同条件下,在该市用丙车比用乙车更省油
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中有7个球,其中4个白球,3个红球,从袋中任意取出2个球,求下列事件的概率:
(1) ![]() 取出的2个球都是白球;
取出的2个球都是白球;
(2)![]() 取出的2个球中1个是白球,另1个是红球.
取出的2个球中1个是白球,另1个是红球.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,坐标原点为
,坐标原点为![]() .椭圆
.椭圆![]() 的动弦
的动弦![]() 过右焦点
过右焦点![]() 且不垂直于坐标轴,
且不垂直于坐标轴, ![]() 的中点为
的中点为![]() ,过
,过![]() 且垂直于线段
且垂直于线段![]() 的直线交射线
的直线交射线![]() 于点
于点![]()
(I)证明:点![]() 在直线
在直线![]() 上;
上;
(Ⅱ)当四边形![]() 是平行四边形时,求
是平行四边形时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的方程为:
的方程为:![]() .
.
(1)直线![]() 过点
过点![]() ,且与圆
,且与圆![]() 交于
交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)圆![]() 上有一动点
上有一动点![]() ,
,![]() ,若向量
,若向量![]() ,求动点
,求动点![]() 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com