练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数f(x)＝4x＋3sinx，x∈(－1，1)，如果f(1－a)＋f(1－a2)<0成立，则实数a的取值范围为(　　)

    A. (0,1) B. C. D. (－∞，－2)∪(1，＋∞)

    【答案】B

    【解析】，在上恒成立， 在上是增函数，又是奇函数，∴不等式可化为，结合函数的定义域可知， 须满足，解得，故选B.

    【方法点晴】本题主要考查函数的定义域、 单调性、奇偶性性，利用单调性解不等式以及导数在函数中的应用，属于难题.根据函数的单调性解不等式应注意以下三点：（1）一定注意抽象函数的定义域（这一点是同学们容易疏忽的地方，不能掉以轻心）；（2）注意应用函数的奇偶性（往往需要先证明是奇函数还是偶函数）；（3）化成 后再利用单调性和定义域列不等式组

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】《孙子算经》是中国古代重要的数学著作，书中有一问题：“今有方物一束，外周一匝有三十二枚，问积几何？”，该著作中提出了一种解决此问题的方法：“重置二位，左位减八，余加右位，至尽虚减一，即得.”通过对该题的研究发现，若一束方物外周一匝的枚数是8的整数倍时，均可采用此方法求解，如图是解决这类问题的程序框图，若输入，则输出的结果为（ ）

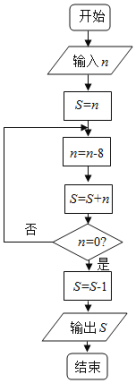
    A.80B.47C.79D.48

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列命题中真命题的个数是　　

    中，是的三内角A，B，C成等差数列的充要条件；

    若“，则”的逆命题为真命题；

    是或充分不必要条件；

    是的充要条件．

    A.1个B.2个C.3个D.4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2019年5月,重庆市育才中学开展了“最美教室”文化布置评比活动,工作人员随机抽取了16间教室进行量化评估,其中评分不低于9分的教室评为优秀,以下表格记录了它们的评分情况:

    分数段

    教室间数

    1

    3

    8

    4

    (1)现从16间教室随机抽取3个,求至多有1个优秀的概率;

    (2)以这16间教室评分数据估计全校教室的布置情况,若从全校所有教室中任选3个,记表示抽到优秀的教室个数,求的分布列及数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】中国古代数学名著《九章算术》中有这样一个问題:今有牛、马、羊食人苗，苗主责之粟五斗，羊主曰:“我羊食半马、“马主曰:“我马食半牛，”今欲衰偿之，问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗，禾苗主人要求赔偿5斗粟、羊主人说:“我羊所吃的禾苗只有马的一半，”马主人说:“我马所吃的禾苗只有牛的一半，“打算按此比例偿还，他们各应偿还多少？该问题中，1斗为10升，则马主人应偿还( )升粟？

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

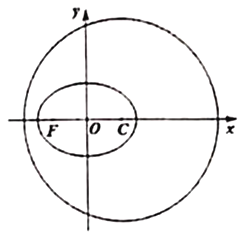
    【题目】已知椭圆的左焦点为，直线与圆交于，两点.

    （1）若直线过点，且，求被椭圆所截得的弦的长度；

    （2）若已知点在椭圆上，动点满足，请判断点与圆的位置关系，并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆：的左、右顶点分别为C、D，且过点，P是椭圆上异于C、D的任意一点，直线PC，PD的斜率之积为．

    （1）求椭圆的方程；

    （2）O为坐标原点，设直线CP交定直线x = m于点M，当m为何值时，为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（，为自然对数的底数，）.

    （1）讨论函数的单调性；

    （2）当时，求使得恒成立的最小整数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】南宋数学家杨辉在《详解九章算法》和《算法通变本末》中，提出了一些新的垛积公式，所讨论的高阶等差数列与一般等差数列不同，前后两项之差并不相等，但是逐项差数之差或者高次差成等差数列对这类高阶等差数列的研究，在杨辉之后一般称为“垛积术”.现有高阶等差数列，其前7项分别为1，4，8，14，23，36，54，则该数列的第19项为（ ）（注：）

    A.1624B.1024C.1198D.1560

    查看答案和解析>>

    同步练习册答案