
【题目】已知:定义在![]() 上的函数
上的函数![]() 的极大值为
的极大值为![]() .
.
(1)求实数![]() 的值;
的值;
(2)若关于![]() 的不等式
的不等式![]() 有且只有一个整数解,求实数
有且只有一个整数解,求实数![]() 的取值范围.
的取值范围.
 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:
【题目】以下命题:(1)已知三个不同的平面![]() ,
,![]() ,
,![]() ,若
,若![]() ,
,![]() ,则
,则![]() ;(2)若直线
;(2)若直线![]() ,
,![]() 与平面
与平面![]() 所成角都是
所成角都是![]() ,则这两条直线平行;(3)若直线
,则这两条直线平行;(3)若直线![]() ,
,![]() 与平面
与平面![]() 所成角都是
所成角都是![]() ,则这两条直线不可能垂直;(4)设直线
,则这两条直线不可能垂直;(4)设直线![]() 与平面
与平面![]() 相交但不垂直,则在平面
相交但不垂直,则在平面![]() 内有且只有一条直线与直线
内有且只有一条直线与直线![]() 垂直.错误的个数是( )
垂直.错误的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位运动员一起参加赛前培训.现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,记录如下:
甲:82 81 79 78 95 88 93 84
乙:86 85 79 86 84 84 85 91
(Ⅰ)请你运用茎叶图表示这两组数据;
(Ⅱ)若用甲8次成绩中高于85分的频率估计概率,对甲同学在今后的3次测试成绩进行预测,记这3次成绩中高于85分的次数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(Ⅲ)现要从中选派一人参加正式比赛,依据所抽取的两组数据分析,你认为选派哪位选手参加较为合适?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
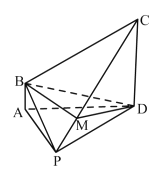
【题目】如图,在四棱锥PABCD-中,AB//CD,AB=1,CD=3,AP=2,DP=2![]() ,PAD=60°,AB⊥平面PAD,点M在棱PC上.
,PAD=60°,AB⊥平面PAD,点M在棱PC上.
(Ⅰ)求证:平面PAB⊥平面PCD;
(Ⅱ)若直线PA// 平面MBD,求此时直线BP与平面MBD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某旅游区拟建一主题游乐园,该游乐区为五边形区域ABCDE,其中三角形区域ABE为主题游乐区,四边形区域为BCDE为休闲游乐区,AB、BC,CD,DE,EA,BE为游乐园的主要道路(不考虑宽度).![]()
![]() .
.

(I)求道路BE的长度;
(Ⅱ)求道路AB,AE长度之和的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过椭圆![]() 右焦点
右焦点![]() 的直线交椭圆与A,B两点,
的直线交椭圆与A,B两点,![]() 为其左焦点,已知
为其左焦点,已知![]() 的周长为8,椭圆的离心率为
的周长为8,椭圆的离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在圆心在原点的圆,使得该圆任意一条切线与椭圆![]() 恒有两个交点
恒有两个交点![]() ,
,![]() ?若存在,求出该圆的方程;若不存在,请说明理由.
?若存在,求出该圆的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com