
【题目】根据下列关系式,算出数列的前4项,然后猜想它的通项,并用数学归纳法证明你的猜想.
(1)![]() ;
;
(2)![]() ;
;
(3)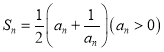 .
.
【答案】(1)![]() ,
,![]() ,证明见解析; (2)
,证明见解析; (2)![]() ,
,![]() ,证明见解析; (3)
,证明见解析; (3)![]() ,
,![]() ,证明见解析.
,证明见解析.
【解析】
分别求出数列的前几项,猜测数列的通项公式,利用数学归纳法,作出证明即可.
(1)由![]() ,
,
令![]() ,则
,则![]() ;令
;令![]() ,则
,则![]() ;令
;令![]() ,则
,则![]() ,
,
由此可猜测数列的通项公式为:![]() ,
,
证明如下:
①当![]() 时,
时,![]() ,显然成立;
,显然成立;
②假设![]() 时,结论成立,即
时,结论成立,即![]() ,
,
则当![]() 时,
时,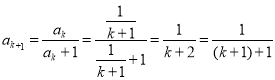 ,
,
即当![]() 时也成立,
时也成立,
由①②可得![]() 对
对![]() 都成,即
都成,即![]() ,
,![]() .
.
(2)由![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() ,即
,即![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() ,即
,即![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() ,即
,即![]() ;
;
猜测数列的通项公式为:![]() ,
,
证明如下:
①当![]() 时,
时,![]() ,显然成立;
,显然成立;
②假设![]() 时,结论成立,即
时,结论成立,即![]() ,
,
则当![]() 时,
时,![]() ,且
,且![]() ,
,
两式相减可得![]() ,即
,即![]() ,
,
整理得![]() ,
,
即当![]() 时也成立,
时也成立,
由①②可得![]() 对
对![]() 都成,即
都成,即![]() ,
,![]() .
.
(3)由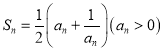 ,
,
令![]() ,可得
,可得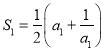 ,即
,即 ,因为
,因为![]() ,则
,则![]() ;
;
令![]() ,可得
,可得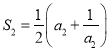 ,即
,即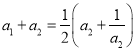 ,解得
,解得![]() ;
;
令![]() ,可得
,可得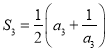 ,即
,即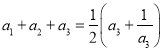 ,解得
,解得![]() ;
;
令![]() ,可得
,可得 ,即
,即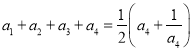 ,解得
,解得![]() ;
;
猜测数列的通项公式为:![]() .
.
证明如下:
①当![]() 时,
时,![]() ,命题成立;
,命题成立;
②假设![]() 时,结论成立,即
时,结论成立,即![]() ,
,
则当![]() 时,
时,![]()
![]() ,
,
所以![]() ,解得
,解得![]() ,
,
即当![]() 时也成立,
时也成立,
由①②可得![]() 对
对![]() 都成,即
都成,即![]() ,
,![]() .
.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:
【题目】下图是2020年2月15日至3月2日武汉市新增新冠肺炎确诊病例的折线统计图.则下列说法不正确的是( )

A.2020年2月19日武汉市新增新冠肺炎确诊病例大幅下降至三位数
B.武汉市在新冠肺炎疫情防控中取得了阶段性的成果,但防控要求不能降低
C.2020年2月19日至3月2日武汉市新增新冠肺炎确诊病例低于400人的有8天
D.2020年2月15日到3月2日武汉市新增新冠肺炎确诊病例最多的一天比最少的一天多1549人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位6个员工借助互联网开展工作,每个员工上网的概率都是0.5(相互独立).至少3人同时上网的概率为________;至少________人同时上网的概率小于0.3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线C的渐近线方程为![]() ,一个焦点为F(0,﹣8),则该双曲线的标准方程为_____.已知点A(﹣6,0),若点P为C上一动点,且P点在x轴上方,当点P的位置变化时,△PAF的周长的最小值为_____.
,一个焦点为F(0,﹣8),则该双曲线的标准方程为_____.已知点A(﹣6,0),若点P为C上一动点,且P点在x轴上方,当点P的位置变化时,△PAF的周长的最小值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣tx+t.
(1)讨论f(x)的单调性;
(2)当t=2时,方程f(x)=m﹣ax恰有两个不相等的实数根x1,x2,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:![]() 的焦点为F,直线y=4与y轴的交点为P,与C的交点为Q,且
的焦点为F,直线y=4与y轴的交点为P,与C的交点为Q,且![]() .
.
(1)求抛物线C的方程;
(2)过F的直线l与C相交于A,B两点,若AB的垂直平分线![]() 与C相交于M,N两点,且A,M,B,N四点在同一个圆上,求直线l的方程.
与C相交于M,N两点,且A,M,B,N四点在同一个圆上,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在某海岸P的附近有三个岛屿Q,R,S,计划建立三座独立大桥,将这四个地方连起来,每座桥只连接两个地方,且不出现立体交叉形式,则不同的连接方式有( ).
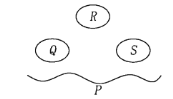
A.24种B.20种C.16种D.12种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在30瓶饮料中,有3瓶已过了保质期.从这30瓶饮料中任取2瓶,则至少取到一瓶已过保质期的概率为 _________ .(结果用最简分数表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com