
分析 (1)求导数,利用导数的正负求函数f(x)的单调区间;
(2)若函数f(x)的图象与直线y=12x相切,求出切点坐标,即可求a的值;
(3)设F(x)=f(x)-12x,则题设可转化为判断函数F(x)在(0,+∞)上是否存在两个零点m,n.
解答 解:(1)f'(x)=6x2+6x=6x(x+1). (1分)
令f'(x)=0,得x1=-1,x2=0,列表如下:
| x | (-∞,-1) | -1 | (-1,0) | 0 | (0,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | 单调递增↗ | 极大值 | 单调递减↘ | 极小值 | 单调递增↗ |
点评 本题考查导数知识的综合运用,考查导数的几何意义,考查函数的单调性,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
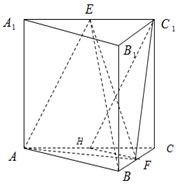 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB=AC,E,F,H分别是A1C1,BC,AC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB=AC,E,F,H分别是A1C1,BC,AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | 1 | C. | $\frac{5}{4}$ | D. | $\frac{7}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱椎P-ABC中,D,E,F分别是棱PC、AC、AB的中点,且PA⊥面ABC.
如图,在三棱椎P-ABC中,D,E,F分别是棱PC、AC、AB的中点,且PA⊥面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 截两坐标轴所得弦的长度相等 | B. | 与两坐标轴都相切 | ||
| C. | 与两坐标轴相离 | D. | 上述情况都有可能 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com