
【题目】【2017湖南长沙二模】已知函数![]() ,
,![]() .
.
(1)证明:![]() ,直线
,直线![]() 都不是曲线
都不是曲线![]() 的切线;
的切线;
(2)若![]() ,使
,使![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)若直线![]() 与曲线
与曲线![]() 相切,因直线
相切,因直线![]() 过定点
过定点![]() ,若设切点
,若设切点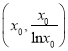 则可得
则可得![]() ①,又
①,又![]() ,
,![]() 上单调递增,当且仅当
上单调递增,当且仅当![]() 时,①成立,这与
时,①成立,这与![]() 矛盾,结论得证.
矛盾,结论得证.
(2)![]() 可转化为
可转化为![]() ,令
,令![]() ,
,![]() ,
,![]() ,分类讨论求
,分类讨论求![]() 的最小值即可.
的最小值即可.
试题解析:(1)![]() 的定义域为
的定义域为![]() ,
,![]() ,直线
,直线![]() 过定点
过定点![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相切于点
相切于点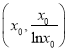 (
(![]() 且
且![]() ),则
),则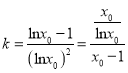 ,即
,即![]() ①,设
①,设![]() ,
,![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,从而当且仅当
,从而当且仅当![]() 时,①成立,这与
时,①成立,这与![]() 矛盾.
矛盾.
所以,![]() ,直线
,直线![]() 都不是曲线
都不是曲线![]() 的切线;
的切线;
(2)![]() 即
即![]() ,令
,令![]() ,
,![]() ,
,
则![]() ,使
,使![]() 成立
成立![]() ,
,
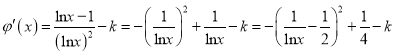 .
.
(i)当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为减函数,于是
上为减函数,于是![]() ,由
,由![]() 得
得![]() ,满足
,满足![]() ,所以
,所以![]() 符合题意;
符合题意;
(ii)当![]() 时,由
时,由![]() 及
及![]() 的单调性知
的单调性知![]() 在
在![]() 上为增函数,所以
上为增函数,所以![]() ,即
,即![]() .
.
①若![]() ,即
,即![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 为增函数,于是
为增函数,于是![]() ,不合题意;
,不合题意;
②若![]() ,即
,即![]() ,则由
,则由![]() ,
,![]() 及
及![]() 的单调性知存在唯一
的单调性知存在唯一![]() ,使
,使![]() ,且当
,且当![]() 时,
时,![]() ,
,![]() 为减函数;当
为减函数;当![]() 时,
时,![]() ,
,![]() 为增函数;
为增函数;
所以![]() ,由
,由![]() 得
得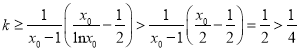 ,这与
,这与![]() 矛盾,不合题意.
矛盾,不合题意.
综上可知,![]() 的取值范围是
的取值范围是![]() .
.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( ) 
A.588
B.480
C.450
D.120
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,PM,切点为Q,M,且满足|PQ|=|PA|. 
(1)求实数a,b间满足的等量关系;
(2)若以P为圆心的圆P与圆O有公共点,试求圆P的半径最小时圆P的方程;
(3)当P点的位置发生变化时,直线QM是否过定点,如果是,求出定点坐标,如果不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆N经过点A(3,1),B(﹣1,3),且它的圆心在直线3x﹣y﹣2=0上.
(Ⅰ)求圆N的方程;
(Ⅱ)求圆N关于直线x﹣y+3=0对称的圆的方程.
(Ⅲ)若点D为圆N上任意一点,且点C(3,0),求线段CD的中点M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正项数列{an}的前n项和Sn满足:Sn2﹣(n2+n﹣1)Sn﹣(n2+n)=0
(1)求数列{an}的通项公式an;
(2)令bn= ![]() ,求数列{bn}的前n项和Tn , 证明:对于任意的n∈N* , 都有Tn
,求数列{bn}的前n项和Tn , 证明:对于任意的n∈N* , 都有Tn ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
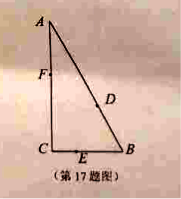
【题目】【2017镇江一模】如图,某公园有三条观光大道![]() 围成直角三角形,其中直角边
围成直角三角形,其中直角边![]() ,
,
斜边![]() .现有甲、乙、丙三位小朋友分别在
.现有甲、乙、丙三位小朋友分别在![]() 大道上嬉戏,所在位
大道上嬉戏,所在位
置分别记为点![]() .
.
(1)若甲乙都以每分钟![]() 的速度从点
的速度从点![]() 出发在各自的大道上奔走,到大道的另一端
出发在各自的大道上奔走,到大道的另一端
时即停,乙比甲迟![]() 分钟出发,当乙出发
分钟出发,当乙出发![]() 分钟后,求此时甲乙两人之间的距离;
分钟后,求此时甲乙两人之间的距离;
(2)设![]() ,乙丙之间的距离是甲乙之间距离的
,乙丙之间的距离是甲乙之间距离的![]() 倍,且
倍,且![]() ,请将甲
,请将甲
乙之间的距离![]() 表示为
表示为![]() 的函数,并求甲乙之间的最小距离.
的函数,并求甲乙之间的最小距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com