
【题目】在数列{an}中,已知a1= ![]() ,an+1=
,an+1= ![]() an﹣
an﹣ ![]() ,n∈N* , 设Sn为{an}的前n项和.
,n∈N* , 设Sn为{an}的前n项和.
(1)求证:数列{3nan}是等差数列;
(2)求Sn;
(3)是否存在正整数p,q,r(p<q<r),使Sp , Sq , Sr成等差数列?若存在,求出p,q,r的值;若不存在,说明理由.
【答案】
(1)证明:由an+1= ![]() an﹣
an﹣ ![]() ,n∈N*,
,n∈N*,
得到3n+1an+1=3nan﹣2,
则3n+1an+1﹣3nan=﹣2.
又∵a1= ![]() ,
,
∴3×a1=1,
数列{3nan}是以1为首项,以﹣2为公差的等差数列
(2)解:由(1)可以推知:3nan=1﹣2(n﹣1),
所以,an= ![]() ,
,
所以Sn= ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() ﹣…﹣
﹣…﹣ ![]() ,①
,①
![]() Sn=
Sn= ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() ﹣…﹣
﹣…﹣ ![]() ,②
,②
①﹣②,得
![]() Sn=
Sn= ![]() ﹣2(
﹣2( ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() )﹣
)﹣ ![]() ,
,
= ![]() ﹣2×
﹣2× 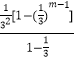 ﹣
﹣ ![]() ,
,
= ![]() ,
,
所以Sn= ![]()
(3)解:假设存在正整数p,q,r(p<q<r),使Sp,Sq,Sr成等差数列.
则2Sq=Sp+Sr,
即 ![]() =
= ![]() +
+ ![]() .
.
由于当n≥2时,an= ![]() <0,
<0,
所以数列{Sn}单调递减.
又p<q,
所以p≤q﹣1且q至少为2,
所以 ![]() ≥
≥ ![]() ,
, ![]() ﹣
﹣ ![]() =
= ![]() .
.
①当q≥3时, ![]() ≥
≥ ![]() ≥
≥ ![]() ,
,
又 ![]() >0,
>0,
所以 ![]() <
< ![]() +
+ ![]() ,等式不成立.
,等式不成立.
②当q=2时,p=1,
所以 ![]() =
= ![]() +
+ ![]() .
.
所以 ![]() =
= ![]() ,
,
所以r=3,(数列{Sn}单调递减,解唯一确定).
综上可知,p,q,r的值分别是1,2,3
【解析】(1)把给出的数列递推式an+1= ![]() an﹣
an﹣ ![]() ,n∈N* , 变形后得到新数列{3nan},该数列是以1为首项,以﹣2为公差的等差数列;(2)由(1)推出{an}的通项公式,利用错位相减法从而求得求Sn;(3)根据等差数列的性质得到2Sq=Sp+Sr , 从而推知p,q,r的值.
,n∈N* , 变形后得到新数列{3nan},该数列是以1为首项,以﹣2为公差的等差数列;(2)由(1)推出{an}的通项公式,利用错位相减法从而求得求Sn;(3)根据等差数列的性质得到2Sq=Sp+Sr , 从而推知p,q,r的值.
【考点精析】利用等差关系的确定和数列的前n项和对题目进行判断即可得到答案,需要熟知如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,即![]() -
-![]() =d ,(n≥2,n∈N
=d ,(n≥2,n∈N![]() )那么这个数列就叫做等差数列;数列{an}的前n项和sn与通项an的关系
)那么这个数列就叫做等差数列;数列{an}的前n项和sn与通项an的关系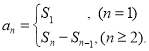 .
.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Ω是一个与x轴的正半轴、y轴的正半轴分别相切于点C、D的定圆所围成区域(含边界),A、B、C、D是该圆的四等分点,若点P(x,y)、P′(x′,y′)满足x≤x′且y≥y′,则称P优于P′,如果Ω中的点Q满足:不存在Ω中的其它点优于Q,那么所有这样的点Q组成的集合是劣弧( ) 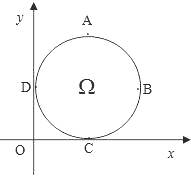
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,若
中,若![]() 是线段
是线段![]() 上的动点,则下列结论不正确的是( )
上的动点,则下列结论不正确的是( )

A. 三棱锥![]() 的正视图面积是定值
的正视图面积是定值
B. 异面直线![]() 所成的角可为
所成的角可为![]()
C. 三棱锥![]() 的体积大小与点
的体积大小与点![]() 在线段
在线段![]() 的位置有关
的位置有关
D. 直线![]() 与平面
与平面![]() 所成的角可为
所成的角可为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列{an}满足:a1=1,an+1=ran+r(n∈N* , 实数r是非零常数),则“r=1”是“数列{an}是等差数列”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一种画椭圆的工具如图1所示.O是滑槽AB的中点,短杆ON可绕O转动,长杆MN通过N处铰链与ON连接,MN上的栓子D可沿滑槽AB滑动,且DN=ON=1,MN=3,当栓子D在滑槽AB内作往复运动时,带动N绕O转动,M处的笔尖画出的椭圆记为C,以O为原点,AB所在的直线为x轴建立如图2所示的平面直角坐标系. 
(1)求椭圆C的方程;
(2)设动直线l与两定直线l1:x﹣2y=0和l2:x+2y=0分别交于P,Q两点.若直线l总与椭圆C有且只有一个公共点,试探究:△OPQ的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com