
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为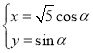 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,求
上,求![]() 的最小值及此时
的最小值及此时![]() 的直角坐标.
的直角坐标.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
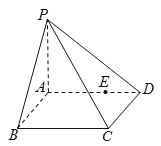
【题目】如图,四棱锥![]() 中,
中,![]() 是矩形,
是矩形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,四棱锥外接球的球心为
,四棱锥外接球的球心为![]() ,点
,点![]() 是棱
是棱![]() 上的一个动点.给出如下命题:①直线
上的一个动点.给出如下命题:①直线![]() 与直线
与直线![]() 是异面直线;②
是异面直线;②![]() 与
与![]() 一定不垂直;③三棱锥
一定不垂直;③三棱锥![]() 的体积为定值;④
的体积为定值;④![]() 的最小值为
的最小值为![]() .其中正确命题的序号是______________.(将你认为正确的命题序号都填上)
.其中正确命题的序号是______________.(将你认为正确的命题序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游景区的景点![]() 处和
处和![]() 处之间有两种到达方式,一种是沿直线步行,另一种是沿索道乘坐缆车,现有一名游客从
处之间有两种到达方式,一种是沿直线步行,另一种是沿索道乘坐缆车,现有一名游客从![]() 处出发,以
处出发,以![]() 的速度匀速步行,
的速度匀速步行,![]() 后到达
后到达![]() 处,在
处,在![]() 处停留
处停留![]() 后,再乘坐缆车回到
后,再乘坐缆车回到![]() 处.假设缆车匀速直线运动的速度为
处.假设缆车匀速直线运动的速度为![]() .
.
(1)求该游客离景点![]() 的距离
的距离![]() 关于出发后的时间
关于出发后的时间![]() 的函数解析式,并指出该函数的定义域;
的函数解析式,并指出该函数的定义域;
(2)做出(1)中函数的图象,并求该游客离景点![]() 的距离不小于
的距离不小于![]() 的总时长.
的总时长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某工厂生产的一种产品的尺寸是否合格,现从500件产品中抽出10件进行检验先将500件产品编号为000,001,002,![]() ,499,在随机数表中任选一个数开始,例如选出第6行第8列的数4开始向右读
,499,在随机数表中任选一个数开始,例如选出第6行第8列的数4开始向右读![]() 为了便于说明,下面摘取了随机数表,附表1的第6行至第8行
为了便于说明,下面摘取了随机数表,附表1的第6行至第8行![]() ,即第一个号码为439,则选出的第4个号码是( )
,即第一个号码为439,则选出的第4个号码是( )
162277943949544354821737932378
844217533157245506887704744767
630163785916955567199810507175
A.548B.443C.379D.217
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】冬季昼夜温差大小与某反季节大豆新品种发芽多少之间有关系,某农科所对此关系进行了调查分析,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:
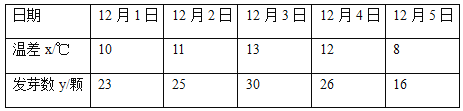
该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)求选取的2组数据恰好是相邻2天数据的概率;
(2)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出y关于x的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
(参考公式: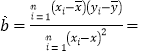 ,
,![]() .)
.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com